 |
A B. 4090. feladat (2008. április) |
B. 4090. Az ABC hegyesszögű háromszög A-ból induló f szögfelezője a BC oldalt D-ben, a köré írható kört E-ben metszi. A C-ből induló magasságvonal f-et M-ben, a köré írható kört Q-ban, a B-ből induló magasságvonal f-et N-ben, a köré írható kört P-ben metszi. Igazoljuk, hogy ekkor
(4 pont)
A beküldési határidő 2008. május 15-én LEJÁRT.
Megoldás: A szokásos jelöléseken túl még jelöljük 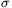 -val, illetve
-val, illetve  -val a PAE és a QAE szögeket. Ha a kör sugara R, akkor PE=2Rsin
-val a PAE és a QAE szögeket. Ha a kör sugara R, akkor PE=2Rsin 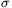 és QE=2Rsin
és QE=2Rsin  , vagyis
, vagyis
Az APN háromszögben az NP oldallal szemközti szög 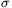 , míg a kerületi szögek tétele miatt az AN oldallal szemközti APB szög
, míg a kerületi szögek tétele miatt az AN oldallal szemközti APB szög  . Ezért a szinusz tétel szerint
. Ezért a szinusz tétel szerint
Mivel a CEM háromszög hasonló az AQM háromszöghöz, az előzőhöz hasonló módon
Ezért
a szögfelező tétel miatt.

Statisztika:
47 dolgozat érkezett. 4 pontot kapott: Anda Roland, Angyal Levente, Balázs Barbara Anna, Bencs 111 Ferenc, Blázsik Zoltán, Bodor Bertalan, Csere Kálmán, Dinh Van Anh, Éles András, Énekes Péter, Fonyó Dávid, Gyurcsik Judit, Huszár Kristóf, Keresztfalvi Tibor, Kiss 902 Melinda Flóra, Kovács 729 Gergely, Kovács 999 Noémi, Lovas Lia Izabella, Márkus Bence, Mester Márton, Molnár 001 Anikó, Molnár Gabriella, Müller Márk, Nagy 648 Donát, Perjési Gábor, Piller Éva, Somogyi Ákos, Szakács Enikő, Tossenberger Anna, Varga 171 László, Weisz Ágoston, Welsz Edit, Zieger Milán, Zsupanek Alexandra. 3 pontot kapott: Cséke Balázs, Dinh Hoangthanh Attila, Dudás 002 Zsolt, Gőgös Balázs, Hursán Zsófia, Márki Róbert, Pasztuhov Anna, Szalkai Balázs, Tóth 369 László Márton, Zelena Réka. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2008. áprilisi matematika feladatai
