A B. 4644. feladat (2014. szeptember)

B. 4644. Egy \(\displaystyle R\) sugarú félkörbe két \(\displaystyle r\) sugarú, egymást kívülről, a félkörívet és az átmérőt pedig belülről érintő kört írtunk az ábra szerint. Határozzuk meg az \(\displaystyle r\) sugarat.

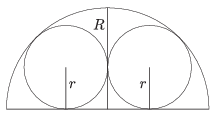
(3 pont)

A beküldési határidő 2014. október 10-én LEJÁRT.

Megoldás. Húzzuk meg az \(\displaystyle r\) és \(\displaystyle R\) sugarú körök közös érintőit, és hosszabbítsuk meg az \(\displaystyle R\) sugarú kör adott átmérőjét mindkét irányban.

A keletkező \(\displaystyle BCD\) háromszöget tükrözzük a \(\displaystyle BD\) átfogójára. Az így létrejött \(\displaystyle ABCD\) négyszög nyilvánvalóan négyzet, oldalai 2\(\displaystyle R\) hosszúak. A négyzet területe: \(\displaystyle T_{ABCD}=4R^{2}\). Az \(\displaystyle SBC\) háromszög területe:

\(\displaystyle T_{SBC\triangle}= \frac{T_{ABCD}}{4}=R^{2}. \)

A Pitagorasz-tételt használva a négyzet átlója:

\(\displaystyle AC=\sqrt {{(2R)}^{2}+{(2R)}^{2}} =\sqrt {8R^{2}} =2\sqrt 2\, R, \)

amiből

\(\displaystyle SB=SC=\frac{AC}{2}=\sqrt 2\, R. \)

\(\displaystyle T_{SBC\triangle}=r\cdot s\), ahol \(\displaystyle s\) a félkerület:

\(\displaystyle s=\frac{SB+SC+BC}{2}=\frac{\sqrt 2\, R+\sqrt 2\, R+2R}{2}=\sqrt 2\, R+R=R \big(\sqrt 2\, +1\big). \)

Ebből

\(\displaystyle r=\frac{T_{SBC\triangle}}{s}=\frac{R^{2}}{R \big(\sqrt 2\, +1\big)}= \frac{R}{\big(\sqrt 2\, +1\big)}\cdot \frac{\big(\sqrt 2\, -1\big)}{\big(\sqrt 2\, -1\big)}= \frac{\big(\sqrt 2\, -1\big)R}{2-1}= \big(\sqrt 2\, -1\big)R. \)

Tehát az \(\displaystyle r\) sugár hossza \(\displaystyle \big(\sqrt 2\, -1\big)R\).

Somogyi Pál (Somorja, Madách Imre Gimn., 11. évf.) dolgozata alapján

Statisztika:

308 dolgozat érkezett.
3 pontot kapott:	221 versenyző.
2 pontot kapott:	61 versenyző.
1 pontot kapott:	20 versenyző.
0 pontot kapott:	5 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2014. szeptemberi matematika feladatai