 |
A B. 4923. feladat (2018. január) |
B. 4923. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló belső szögfelezője a \(\displaystyle BC\) oldalt \(\displaystyle E\)-ben, a \(\displaystyle B\)-ből induló belső szögfelezője az \(\displaystyle AC\) oldalt \(\displaystyle F\)-ben metszi. Jelölje \(\displaystyle O\) a háromszög beírt körének középpontját. Mekkora lehet a \(\displaystyle C\)-nél levő szög, ha az \(\displaystyle OFA\triangle\) és a \(\displaystyle OBE\triangle\) területének összege egyenlő az \(\displaystyle AOB\triangle\) területével?
(3 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
1. megoldás. Használjuk az ábra jelöléseit. A beírt kör sugara legyen \(\displaystyle r\).

A szögfelező tételt felhasználva:
\(\displaystyle AF=b\cdot \frac{c}{a+c}\mathrm{~és~} BE=a\cdot \frac{c}{b+c}.\)
\(\displaystyle T_{AOB}=c\cdot \frac r2,\)
\(\displaystyle T_{OFA}=AF\cdot \frac r2=\frac{b}{a+c}\cdot c\cdot\frac r2,\)
\(\displaystyle T_{OBE}=BE\cdot \frac r2=\frac{a}{b+c}\cdot c\cdot\frac r2.\)
\(\displaystyle T_{AOB}=T_{OFA}+T_{OBE},\)
vagyis
\(\displaystyle c\cdot \frac r2=\frac{b}{a+c}\cdot c\cdot\frac r2+\frac{a}{b+c}\cdot c\cdot\frac r2.\)
Leosztva \(\displaystyle c\cdot \frac r2≠0\)-val:
\(\displaystyle 1=\frac{b}{a+c}+\frac{a}{b+c}.\)
Közös nevezőre hozva:
\(\displaystyle 1=\frac{b(b+c)+a(a+c)}{(a+c)(b+c)}.\)
Szorozzuk be mindkét oldalt az \(\displaystyle (a+c)(b+c)>0\) kifejezéssel és bontsuk fel a zárójeleket:
\(\displaystyle ab+ac+bc+c^2=b^2+bc+a^2+ac.\)
Rendezve:
\(\displaystyle c^2=a^2+b^2-ab.\)
Felhasználva a koszinusz-tételt:
\(\displaystyle c^2=a^2+b^2-2ab\cos γ=a^2+b^2-ab,\)
vagyis \(\displaystyle \cos γ=1/2\). Mivel \(\displaystyle 0<γ<180°\), így csak \(\displaystyle γ=60°\) lehet a háromszög \(\displaystyle C\) csúcsnál lévő szöge. Az átalakítások ekvivalensek voltak, tehát \(\displaystyle γ=60°\)esetén telesül a háromszögek területére vonatkozó feltétel.
2. megoldás. Legyenek a háromszög szögei a szokásos módon \(\displaystyle \alpha,\beta,\gamma\), és legyen \(\displaystyle F'\) az \(\displaystyle F\) pont tükörképe az \(\displaystyle AOE\) szögfelezőre. A tükrözés miatt az \(\displaystyle AOF\) és \(\displaystyle AOF'\) háromszögek egybevágók és területük egyenlő. Mivel az \(\displaystyle ABO\) háromszög területe egyenlő az \(\displaystyle AOF\) és \(\displaystyle BEO\) háromszög területének összegével, a \(\displaystyle BOF'\) háromszög területe is megegyezik a \(\displaystyle BEO\) háromszög területével. Ennek a két háromszögnek tehát a területe megegyezik, a \(\displaystyle BO\) oldaluk közös, és a \(\displaystyle B\) csúcsnál ugyanakkora szögük van; ez csak úgy lehet, ha \(\displaystyle BE=BF'\), és a két háromszög egymás tükörképe a \(\displaystyle BOF\) szögfelezőre.
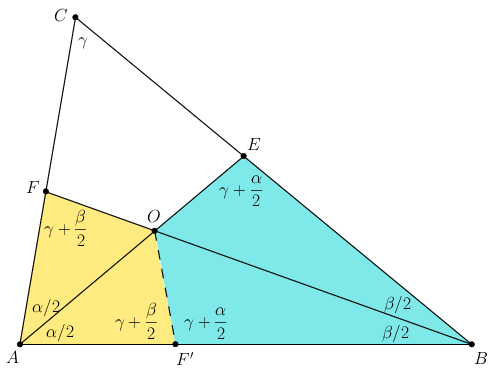
A \(\displaystyle BCF\) és \(\displaystyle AEC\) háromszögek szögeinek összeszámolásából látjuk, hogy
\(\displaystyle OF'A \sphericalangle = AFB\sphericalangle = FCB\sphericalangle + CBF\sphericalangle = \gamma+\frac\beta2 \)
és
\(\displaystyle BF'O \sphericalangle = AEB\sphericalangle = ACE\sphericalangle + EAC\sphericalangle = \gamma+\frac\alpha2. \)
Mivel \(\displaystyle OF'A \sphericalangle + BF'O \sphericalangle = 180^\circ\),
\(\displaystyle \left(\gamma+\frac\beta2\right) + \left(\gamma+\frac\alpha2\right) = 180^\circ \)
\(\displaystyle 2\gamma + \frac{\alpha+\beta}2 = 2\gamma + \frac{180^\circ-\gamma}2 = 180^\circ \)
\(\displaystyle \gamma = 60^\circ. \)
A megoldás teljességéhez hozzá tartozik annak ellenőrzése, hogy létezik a feladat feltételeinek megfelelő \(\displaystyle ABC\) háromszög, tehát az \(\displaystyle \gamma = 60^\circ\) valóban lehetséges.
Vegyük észre, hogy a lépéseink megfordíthatóak: ha a háromszögben \(\displaystyle \gamma=60^\circ\), akkor \(\displaystyle \left(\gamma+\frac\beta2\right) + \left(\gamma+\frac\alpha2\right) = 180^\circ\), így a \(\displaystyle BEO\) és \(\displaystyle BF'O\) háromszögek egybevágóak és egymás tükörképei, emiatt az \(\displaystyle ABO\) háromszög területe megegyezik az \(\displaystyle AOF\) és \(\displaystyle BEO\) háromszögek területösszegével.
Statisztika:
109 dolgozat érkezett. 3 pontot kapott: 71 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 13 versenyző.
A KöMaL 2018. januári matematika feladatai
