A B. 5385. feladat (2024. április)

B. 5385. Az \(\displaystyle ABC\) hegyesszögű háromszögben jelölje \(\displaystyle F\) a Feuerbach-kör középpontját. Bizonyítsuk be, hogy \(\displaystyle AF^2-BF^2=Rc\sin(\beta-\alpha)\), ahol \(\displaystyle R\) a köréírt kör sugarát, \(\displaystyle c\) az \(\displaystyle AB\) oldal hosszát, míg \(\displaystyle \alpha\) és \(\displaystyle \beta\) az \(\displaystyle A\) és \(\displaystyle B\) csúcsoknál levő belső szöget jelöli.

Javasolta: Bencze Mihály (Brassó)

(4 pont)

A beküldési határidő 2024. május 10-én LEJÁRT.

Megoldás. Irányítsunk vektorokat a körülírt kör \(\displaystyle O\) középpontjából a csúcsokba. Legyenek ezek \(\displaystyle \mathbf{a,~ b, ~c}\). Mindhárom vektor hossza a körülírt kör \(\displaystyle R\) sugara.

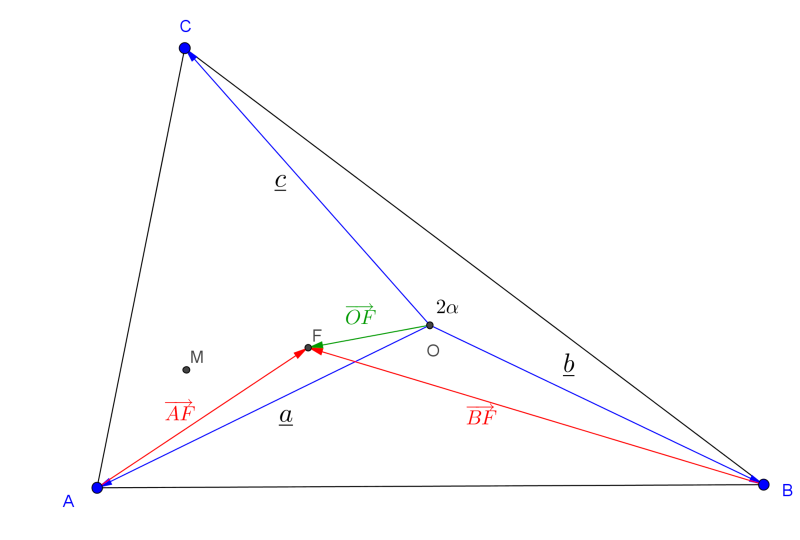
Ismert, hogy ezen három vektor összege a magasságpontba mutat, a Feuerbach-kör \(\displaystyle F\) középpontja pedig felezi az \(\displaystyle OM\) szakaszt, tehát

\(\displaystyle \overrightarrow{OF}=\frac{1}{2}(\mathbf{a}+\mathbf{b}+\mathbf{c}).\)

Eddigi jelöléseinkkel az \(\displaystyle \overrightarrow{AF}\) és \(\displaystyle \overrightarrow{BF}\) vektorok is kifejezhetők:

\(\displaystyle \overrightarrow{AF}=\frac{1}{2}(\mathbf{a}+\mathbf{b}+\mathbf{c})-\mathbf{a}=\frac{1}{2}(\mathbf{b}+\mathbf{c}-\mathbf{a}),\quad \text{illetve} \quad \overrightarrow{BF}=\frac{1}{2}(\mathbf{a}+\mathbf{b}+\mathbf{c})-\mathbf{b}=\frac{1}{2}(\mathbf{a}+\mathbf{c}-\mathbf{b}).\)

A továbbiakban skaláris szorzat segítségével számoljuk ki az \(\displaystyle AF\) és \(\displaystyle BF\) hosszúságok négyzeteinek különbségét:

\(\displaystyle AF^2-BF^2=\frac{1}{4}(\mathbf{b}+\mathbf{c}-\mathbf{a})^2-\frac{1}{4}(\mathbf{a}+\mathbf{c}-\mathbf{b})^2=\frac{(2\mathbf{b}-2\mathbf{a})(2\mathbf{c})}{4}=(\mathbf{b}-\mathbf{a})\mathbf{c}.\)

A zárójel felbontása után felhasználjuk, hogy az \(\displaystyle \mathbf{a,~ b, ~c}\) vektorok egymással bezárt szögei középponti szögek, kétszeresei a háromszög szögeinek: azaz a \(\displaystyle \mathbf{b, ~c}\) vektorok szöge \(\displaystyle 2\alpha\), míg az \(\displaystyle \mathbf{a, ~c}\) vektorok szöge \(\displaystyle 2\beta\).

\(\displaystyle (\mathbf{b}-\mathbf{a})\mathbf{c}=\mathbf{b}\cdot \mathbf{c} - \mathbf{a}\cdot \mathbf{c}=R^2\cos 2\alpha - R^2\cos2\beta=R^2(\cos2\alpha-\cos2\beta).\)

Végül alkalmazzuk a szögek koszinuszainak különbségeire vonatkozó addíciós tételt és a háromszög oldala és a körülírt kör sugara közötti \(\displaystyle c=2R\sin\gamma=2R\sin(\alpha+\beta)\) összefüggést:

\(\displaystyle R^2(\cos2\alpha-\cos2\beta)=-2R^2\sin(\alpha+\beta)\cdot \sin(\alpha-\beta)=2R^2\sin\gamma\cdot \sin(\beta-\alpha)=Rc\sin(\beta-\alpha).\)

Ezzel az állítást beláttuk.

Statisztika:

49 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Aravin Peter, Bencze Mátyás, Bodor Mátyás, Bogdán Balázs Ákos, Bővíz Dániel, Bui Thuy-Trang Nikolett, Christ Miranda Anna, Csonka Illés, Dam Soham, Diaconescu Tashi, Erdélyi Kata, Farkas 005 Bendegúz, Fekete Aron, Fórizs Emma, Forrai Boldizsár, Gömze Norken, Gyenes Károly, Hodossy Réka, Holló Martin, Horák Zsófia, Jármai Roland, Kerekes András, Keresztély Zsófia, Klement Tamás, Kovács Benedek Noel, Kővágó Edit Gréta, Morvai Várkony Albert, Pletikoszity Martin, Prohászka Bulcsú, Puppi Barna, Romaniuc Albert-Iulian, Sánta Gergely Péter, Sárdinecz Dóra, Sha Jingyuan, Sütő Áron, Szabó 721 Sámuel, Török Eszter Júlia, Veres Dorottya, Vigh 279 Zalán, Virág Lénárd Dániel, Virág Tóbiás, Zhai Yu Fan.
3 pontot kapott:	Csupor Albert Dezső, Op Den Kelder Ábel.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2024. áprilisi matematika feladatai