 |
A B. 5392. feladat (2024. május) |
B. 5392. Tekintsünk egy olyan trapézt, amelynek területe egyenlő alapjainak szorzatával. Mutassuk meg, hogy ez a trapéz pontosan akkor érintőnégyszög, ha derékszögű.
Javasolta: Németh László (Fonyód)
(5 pont)
A beküldési határidő 2024. június 10-én LEJÁRT.
Megoldás. Legyenek a trapéz alapjai \(\displaystyle a\) és \(\displaystyle c\) \(\displaystyle (a\ge c)\), szárai \(\displaystyle b\) és \(\displaystyle d\), magassága \(\displaystyle m\).
\(\displaystyle (i)\) Először a területre megadott feltétel alapján a trapéz magasságára adunk egy, a megoldáshoz végig jól használható, ekvivalens feltételt. Az ismert területképletet összevetve a feltétellel:
\(\displaystyle T=ac=\frac{a+c}{2}m, \quad\text{rendezve} \quad m=\frac{2ac}{a+c}, \)
vagyis a terület akkor és a csak akkor az alapok szorzata, ha a magasság az alapok harmonikus közepe.
\(\displaystyle (ii)\) Megmutatjuk, hogy a feltétel szerinti derékszögű trapéz érintőnégyszög. Legyen továbbra is \(\displaystyle a\ge c\) és \(\displaystyle b=m=\frac{2ac}{a+c}\). A \(\displaystyle c\) alapot merőlegesen vetítjük az \(\displaystyle a\) alapra.
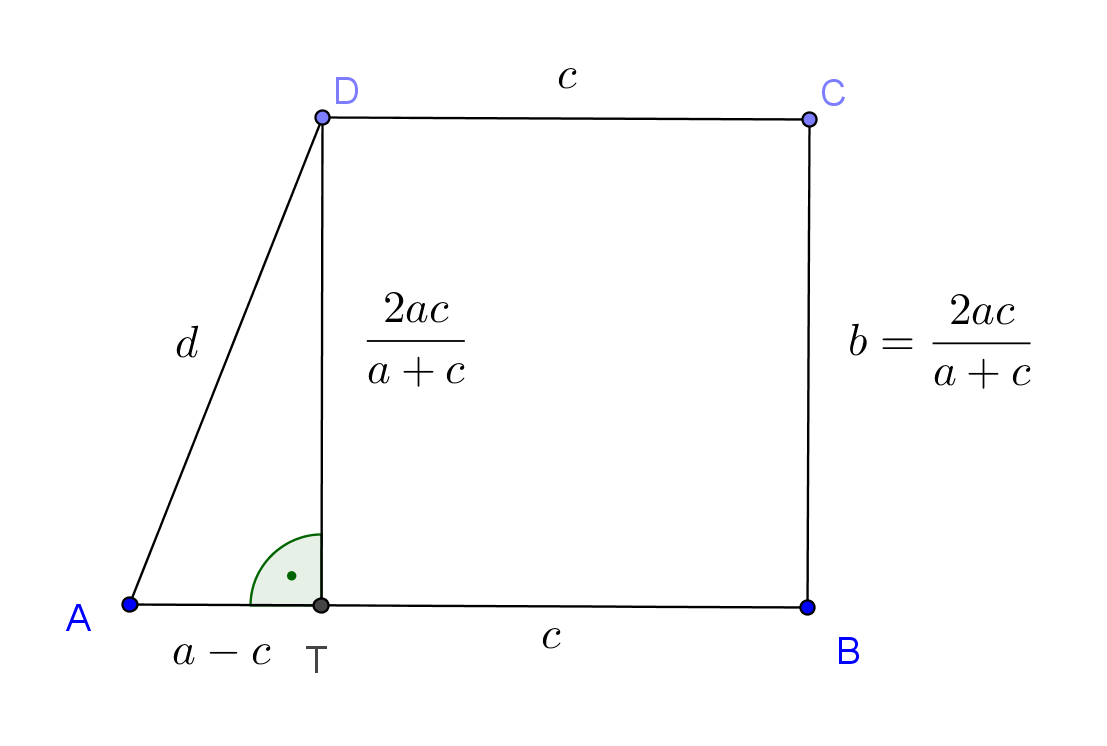
Ezután a \(\displaystyle d\) szárra már alkalmazhatjuk Pitagorasz tételét:
\(\displaystyle d^2=(a-c)^2+\left(\frac{2ac}{a+c}\right)^2=\frac{(a^2-c^2)^2+4a^2c^2}{(a+c)^2}=\frac{a^4-2a^2c^2+c^4+4a^2c^2}{(a+c)^2}=\frac{(a^2+c^2)^2}{(a+c)^2}, ~~\text{azaz} ~~d=\frac{a^2+c^2}{a+c} .\)
Ezután már könnyen ellenőrízhető, hogy valóban érintőnégyszögről van szó:
\(\displaystyle b+d=\frac{2ac}{a+c}+\frac{a^2+c^2}{a+c}=\frac{a^2+c^2+2ac}{a+c}=a+c. \)
Az érintőnégyszögek tétele alapján így a konvex négyszög valóban érintőnégyszög.
Megjegyzés: Az \(\displaystyle a\) és \(\displaystyle c\) pozitív számok esetén \(\displaystyle \frac{2ac}{a+c}\) a harmonikus közép, míg \(\displaystyle \frac{a^2+c^2}{a+c}\) az ún. kontraharmonikus közép.
\(\displaystyle (iii)\) Felhasználva, hogy a trapéz érintőnégyszög, azaz \(\displaystyle a+c=b+d\), és hogy a magasság \(\displaystyle m=\frac{2ac}{a+c}\) megmutatjuk, hogy derékszögű a trapéz.
Ha \(\displaystyle a=c\), akkor a négyszög paralelogramma, sőt \(\displaystyle a+c=b+d\) miatt rombusz. Továbbá \(\displaystyle m=2a^2/(a+a)=a\), amiből \(\displaystyle b=a=m\), és így a négyszög négyzet, azaz az állítás igaz. A továbbiakban feltesszük, hogy \(\displaystyle a>c\).
Húzzunk párhuzamost a trapéz \(\displaystyle C\) csúcsán keresztül az \(\displaystyle AD=d\) szárral. A párhuzamos messe az \(\displaystyle AB=a\) oldalt az \(\displaystyle E\) pontban. Az \(\displaystyle EBC\) háromszög oldalai \(\displaystyle EB=a-c, ~BC=b\), és \(\displaystyle CE=d\).
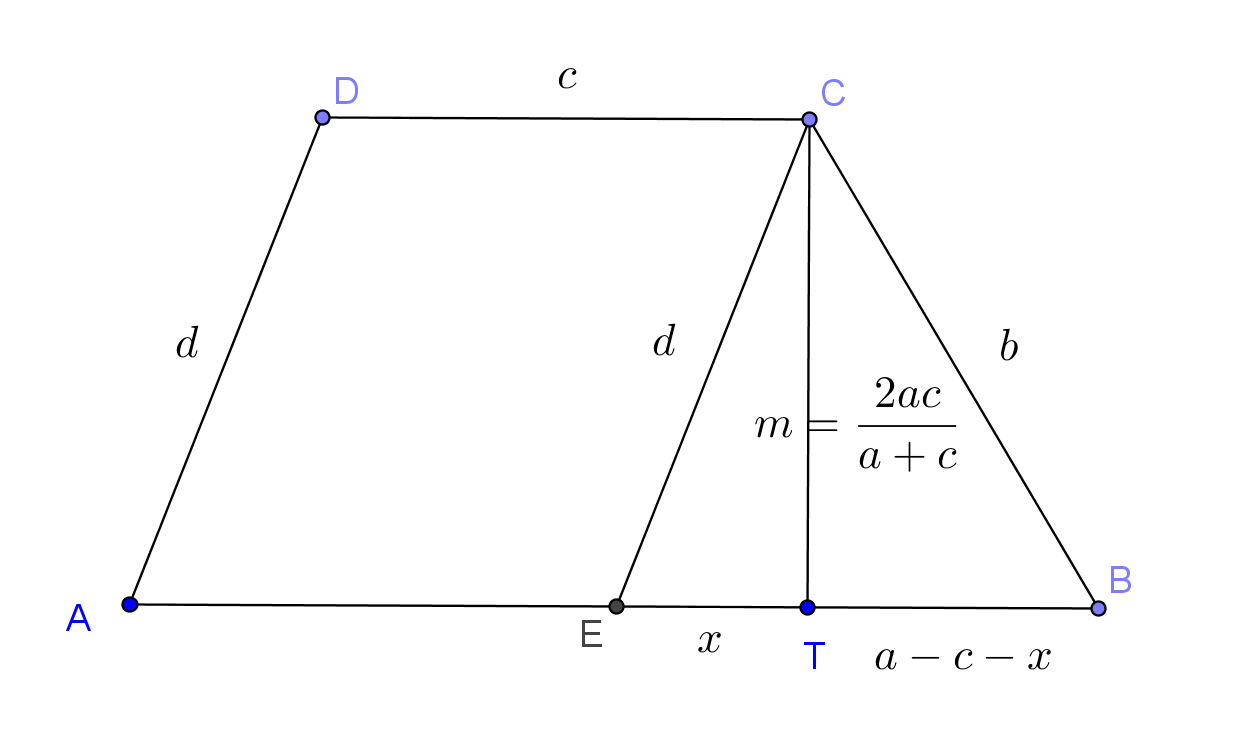
Tudjuk továbbá, hogy ebben a háromszögben a \(\displaystyle C\) csúcshoz tartozó magasság \(\displaystyle m=\frac{2ac}{a+c}\). Legyen e magasság talppontja az \(\displaystyle EB\) oldal egyenesén \(\displaystyle T\). Az \(\displaystyle ET\) és \(\displaystyle TB\) előjeles távolságok pedig \(\displaystyle ET=x\), illetve \(\displaystyle TB=a-c-x\). Most alkalmazzuk a Pitagorasz-tételt az \(\displaystyle ETC\) és \(\displaystyle BTC\) derékszögű háromszögekre:
\(\displaystyle x^2+m^2=d^2,\)
\(\displaystyle (a-c-x)^2+m^2=b^2=(a+c-d)^2.\)
A második egyenlet kifejtésével:
\(\displaystyle (a-c)^2-2x(a-c)+x^2+m^2=(a+c)^2-2d(a+c)+d^2.\)
Tudjuk az első egyenlet alapján, hogy \(\displaystyle x^2+m^2=d^2\), így ki tudjuk fejezni az alapokkal és a \(\displaystyle d\) szárral \(\displaystyle x\)-et.
\(\displaystyle a^2-2ac+c^2-2x(a-c)=a^2+2ac+c^2-2d(a+c), \)
\(\displaystyle -2x(a-c)=4ac-2d(a+c),\)
\(\displaystyle x=d\frac{a+c}{a-c}-\frac{2ac}{a-c}. \)
Ezt beírva az első egyenletbe és most már azt is részletezve, hogy \(\displaystyle m=\frac{2ac}{a+c}\) a \(\displaystyle d\) szárra másodfokú egyenletet kapunk:
\(\displaystyle d^2\frac{(a+c)^2}{(a-c)^2}-\frac{4dac(a+c)}{(a-c)^2}+\frac{4a^2c^2}{(a-c)^2}+\frac{4a^2c^2}{(a+c)^2}=d^2, \)
\(\displaystyle d^2\left(\frac{(a+c)^2}{(a-c)^2}-1\right)- d\frac{4ac(a+c)}{(a-c)^2}+\frac{4a^2c^2(2a^2+2c^2)}{(a-c)^2(a+c)^2}=0.\)
Szorozzuk az egyenletet \(\displaystyle (a-c)^2\)-tel és egyszerűsítsünk \(\displaystyle 4ac\)-vel:
\(\displaystyle d^2-(a+c)d+\frac{2ac(a^2+c^2)}{(a+c)^2}=0.\)
Ennek gyökei – Viéte formuláival ellenőrízhetően – éppen
\(\displaystyle d_1=\frac{2ac}{a+c} \quad \text{és }\quad d_2=\frac{a^2+c^2}{a+c}.\)
Az összegük \(\displaystyle a+c\), így \(\displaystyle b_1=d_2\) és \(\displaystyle b_2=d_1\). Megkaptuk, hogy csak abban az esetben kapunk érintőnégyszöget \(\displaystyle T=ac\) esetén, ha az egyik szár a magassággal egyenlő, vagyis a trapéz derékszögű.
Megjegyzés: Természetesen megoldóképlettel is ugyanezt az eredményt kapjuk, csak több számolással.
\(\displaystyle d_{1,2}=\frac{a+c}{2}\pm \sqrt{\left(\frac{a+c}{2}\right)^2-\frac{2ac(a^2+c^2)}{(a+c)^2}}=\frac{a+c}{2}\pm \sqrt{\frac{(a-c)^4}{4(a+c)^2}}=\)
\(\displaystyle =\frac{a+c}{2}\pm \frac{(a-c)^2}{2(a+c)}=\frac{(a+c)^2\pm (a-c)^2}{2(a+c)}. \)
Kivonással \(\displaystyle d_1=\frac{2ac}{a+c}\), összeadással pedig \(\displaystyle d_2=\frac{a^2+c^2}{a+c}\) adódik.
Statisztika:
54 dolgozat érkezett. 5 pontot kapott: Ali Richárd, Aravin Peter, Bodor Mátyás, Csató Hanna Zita , Diaconescu Tashi, Erdélyi Kata, Forrai Boldizsár, Hodossy Réka, Holló Martin, Kerekes András, Kovács Benedek Noel, Sárdinecz Dóra, Sütő Áron, Szabó 721 Sámuel, Tamás Gellért, Varga 511 Vivien, Vigh 279 Zalán, Virág Tóbiás, Wágner Márton. 4 pontot kapott: Bui Thuy-Trang Nikolett, Csupor Albert Dezső, Dam Soham, Fórizs Emma, Lakner Hanna, Sha Jingyuan, Virág Lénárd Dániel. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. májusi matematika feladatai
