A B. 5396. feladat (2024. május)

B. 5396. Egy egyenlő oldalú térbeli (torz) ötszögnek négy derékszöge van. Mekkora lehet az ötödik szöge?

Javasolta: Dombi Péter (Pécs)

(6 pont)

A beküldési határidő 2024. június 10-én LEJÁRT.

Megoldás. Legyen az ötszögünk \(\displaystyle ABCDE\), és tegyük fel, hogy a derékszögű csúcsok \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\). Válasszuk úgy a koordináta-rendszert, hogy \(\displaystyle A(0,0,0)\), \(\displaystyle B(1,0,0)\) és \(\displaystyle C(1,1,0)\). Mivel \(\displaystyle BCD\sphericalangle=90^\circ\), ezért \(\displaystyle D\) rajta van az \(\displaystyle y=1\) síkon, és így \(\displaystyle t\)-vel jelölve a \(\displaystyle \overrightarrow{CD}\) és \(\displaystyle x\)-tengely szögét kapjuk, hogy \(\displaystyle D(1+\cos t, 1, \sin t)\). Hasonlóan \(\displaystyle E(0,\cos u, \sin u)\), ahol \(\displaystyle u\) az \(\displaystyle \overrightarrow{AE}\) és \(\displaystyle y\)-tengely szöge. (\(\displaystyle D\) és \(\displaystyle E\) egy-egy egységnyi sugarú körön lehet.)

Kettő feltevést nem használtunk még ki, hogy \(\displaystyle D\)-nél is derékszög van, illetve hogy \(\displaystyle DE=1\). Előbbi ekvivalens azzal, hogy \(\displaystyle \overrightarrow{CD}\cdot \overrightarrow{DE}=0\). Mivel \(\displaystyle \overrightarrow{CD}=(\cos t , 0 , \sin t)\), és \(\displaystyle \overrightarrow{DE}=(-1-\cos t, \cos u -1, \sin u -\sin t)\), így a \(\displaystyle -\cos t -\cos^2 t + \sin t \sin u - \sin ^2 t=0\) egyenlethez jutunk, azaz

\(\displaystyle -\cos t + \sin t \sin u =1.\)

Másrészt \(\displaystyle DE=1\)-ből \(\displaystyle (1+\cos t)^2+(1-\cos u)^2+(\sin u -\sin t)^2=1\), amit kibontva és rendezve

\(\displaystyle 2\cos t - 2\cos u - 2 \sin u \sin t=-3.\)

Ezekből \(\displaystyle t\) és \(\displaystyle u\) értéke meghatározható. Az első egyenlet kétszeresét a másodikhoz adva \(\displaystyle \cos u =1/2\) adódik. Feltehetjük, hogy \(\displaystyle u=\pi/3\) (különben tükrözzük az ábrát az \(\displaystyle xy\)-síkra), s így \(\displaystyle E(0,1/2,\sqrt3/2)\).

Visszahelyettesítve \(\displaystyle u\) értékét az \(\displaystyle 1=\sqrt 3/2 \cdot \sin t- \cos t\) egyenletet kapjuk, amiből \(\displaystyle t_1=\pi\) és \(\displaystyle t_2\approx 1,71\). A \(\displaystyle t_1\)-hez a \(\displaystyle D(0,1,0)\) pont tartozik, ekkor az \(\displaystyle ADE\) háromszög szabályos, és a keresett ötödik szög \(\displaystyle 60^\circ\).

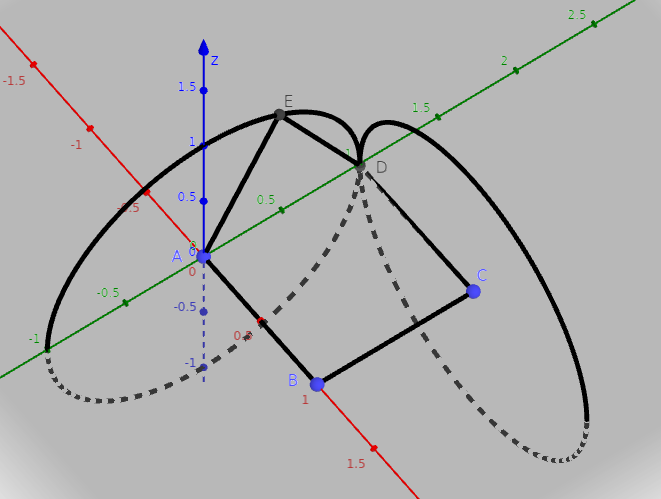
A \(\displaystyle t_2\)-höz a \(\displaystyle D(0,86;1;0,99)\) pont tartozik. Az \(\displaystyle \overrightarrow{EA}\) és \(\displaystyle \overrightarrow{ED}\) szögét leggyorsabban skalárszorzatból határozhatjuk meg, rutin számolás után

\(\displaystyle \cos \varphi=\frac {\overrightarrow{EA}\cdot \overrightarrow{ED}}{|\overrightarrow{EA}|\cdot |\overrightarrow{EA}|}\approx -0,36,\)

amiből a keresett szögre (körülbelül) \(\displaystyle 111^\circ\) adódik.

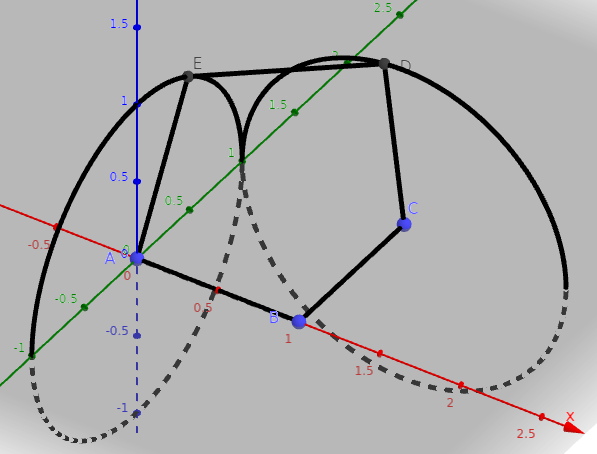
Két megoldást kaptunk, a keresett szög \(\displaystyle 60^\circ\) vagy (körülbelül) \(\displaystyle 111^\circ\) lehet.

Megjegyzések. 1. A számolás közelítések nélkül is elvégezhető trigonometrikus azonosságok felhasználásával, így a második esetre a \(\displaystyle \cos \varphi=-5/14\) pontos érték adódik.

2. Másképp is célt érhetünk: az \(\displaystyle ABE\) és \(\displaystyle CDE\) egyenlő szárú derékszögű háromszögek, emiatt a \(\displaystyle BCE\) háromszög oldalai \(\displaystyle 1\), \(\displaystyle \sqrt 2\), \(\displaystyle \sqrt 2\). Erre az adott háromszögre ,,ragasztjuk rá" az \(\displaystyle ABE\) és \(\displaystyle CDE\) egyenlő szárú, derékszögű háromszögeket úgy, hogy a \(\displaystyle B\), ill. \(\displaystyle C\) csúcsoknál is derékszöge legyen a kapott ötszögnek. Mindkét háromszög két-kétféleképpen ragaszható fel, de a kapott négy ötszögből kettő-kettő egybevágó. A számolás ezek alapján is elvégezhető, de ekkor is célszerű az ábrát valahogy elhelyezni egy koordinátarendszerben. Érdekes megjegyezni, hogy míg az első, \(\displaystyle 60^\circ\)-t adó konstrukció síkra szimmetrikus, addig a második, tompaszögű esetben a két egybevágó megoldás egymás tükörképe (szemléletesen van egy jobbos, és egy balos változat).

Statisztika:

42 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Aravin Peter, Bencze Mátyás, Bodor Mátyás, Bui Thuy-Trang Nikolett, Erdélyi Kata, Hodossy Réka, Keresztély Zsófia, Kovács Barnabás, Kovács Benedek Noel, Pletikoszity Martin, Prohászka Bulcsú, Sárdinecz Dóra, Vigh 279 Zalán, Virág Tóbiás, Wágner Márton.
5 pontot kapott:	Christ Miranda Anna, Dam Soham, Gyenes Károly, Holló Martin, Tulkán Dávid, Veres Dorottya.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2024. májusi matematika feladatai