A C. 1119. feladat (2012. március)

C. 1119. Az ábrán látható módon a rövidebb, 10 cm hosszú befogójuk mentén egymáshoz rögzítettünk két egyforma (30-60 fokos) derékszögű vonalzót, majd az alakzat tetejére tettünk egy egyenlő szárú derékszögűt is. Elférne-e az így kapott tetraéder belsejében egy 3,2 cm sugarú teniszlabda?

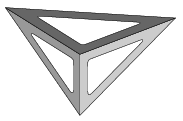
(5 pont)

A beküldési határidő 2012. április 10-én LEJÁRT.

Megoldás. Az egyenlő szárú derékszögű vonalzó befogójának hossza \(\displaystyle \frac{\sqrt 3}2 \cdot 10\) cm hosszú, a vonalzók alkotta tetraéder térfogata pedig \(\displaystyle \frac{1}{6}\cdot 10\cdot 10\cdot \frac{\sqrt 3}2 \cdot 10=\frac{1000\sqrt 3}{12}cm^3\approx 144,3cm^3\). A tetraéderbe írható gömb sugara \(\displaystyle r\), akkor a térfogata kiszámolható \(\displaystyle \frac{1}{3}A\cdot r\)-ként is. A vonalzók alkotta tetraéder negyedik lapjának oldalai \(\displaystyle 20cm\), \(\displaystyle 20cm\) és \(\displaystyle \frac{\sqrt 6}2 \cdot 10 cm\) hosszúak, területe (pl. Heron-képletet alkalmazva) \(\displaystyle \frac{25\sqrt{15}}{2}cm^2\). A felszín tehát \(\displaystyle A=\frac{\sqrt 3}{8}\cdot 100 + \frac{\sqrt 3}{4}\cdot 100 + \frac{3}{8}\cdot 100 + \frac{\sqrt{15}}{8}\cdot 100 \approx 172,5 cm^2\). A tetraéderbe írható gömb sugara tehát \(\displaystyle r\approx 3,58 cm\), vagyis belefér a vonalzók alkotta tetraéderbe egy 3,2 cm sugarú teniszlabda.

Statisztika:

156 dolgozat érkezett.
5 pontot kapott:	90 versenyző.
4 pontot kapott:	12 versenyző.
3 pontot kapott:	26 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2012. márciusi matematika feladatai