A C. 1287. feladat (2015. április)

C. 1287. Egy elég nagy négyzethálós lapra csigavonalban haladva felírjuk a pozitív egész számokat az ábra szerint. Melyik számok állnak a 2015 felett és alatt?

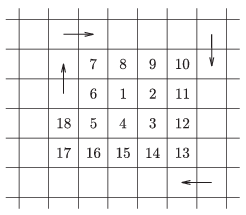
(5 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldás. Az ábrán bejelölt négyzetek oldala 2, illetve 4 hosszú, a bal alsó mezőben \(\displaystyle 2^2\), illetve \(\displaystyle 4^2\) áll. Ha a számozást folytatjuk, akkor a páros négyzetszámok sorban a következő négyzet bal alsó mezőjébe kerülnek.

Hasonlóan, a következő ábrán a páratlan négyzetszámok vannak pirossal megjelölve, azok mindig a soron következő négyzet jobb felső sarkába kerülnek.

Mivel \(\displaystyle 2015=2025-10=45^2-10\), ezért a 2015 fölött a \(\displaystyle 47^2-11=2198\) áll, alatta pedig a \(\displaystyle 43^2-9=1840\).

Statisztika:

95 dolgozat érkezett.
5 pontot kapott:	Ardai István Tamás, Balázs Ákos Miklós, Banczik Zoltán Ádám, Bindics Boldizsár, Csapó Márton, Erdélyi Janka, Fekete Balázs Attila, Glasznova Maja, Horváth Botond, Hunyadi Marcell, Jakus Balázs István, Kamenár Gyöngyvér, Klász Viktória, Kocsis Júlia, Kormányos Hanna Rebeka, Mamuzsics Gergő Bence, Marozsák Tóbiás , Márton Dénes, Móricz Benedek, Nagy 911 Viktória, Nagy Enikő, Németh 417 Tamás, Páhoki Tamás, Schrettner Jakab, Sebastian Fodor, Souly Alexandra, Szabó Alexandra, Szűcs 865 Eszter, Temesvári Bence, Tevesz Judit, Török Ádám, Ványi Virág, Varga-Umbrich Eszter, Veres Károly.
4 pontot kapott:	29 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. áprilisi matematika feladatai