 |
A C. 1305. feladat (2015. szeptember) |
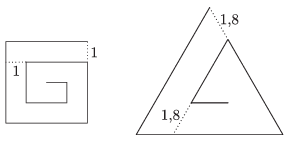
C. 1305. Egy \(\displaystyle n\) egység oldalú négyzetből spirált készítünk az ábrán látható módon úgy, hogy a négyzet csúcsából indulva, befelé haladva mindig egy egységgel azelőtt törjük meg a vonalat, minthogy az belemetszene a spirál már meglévő részébe. Hasonló módon az \(\displaystyle 1{,}8n\) egység oldalú szabályos háromszögből képzett spirálnál a metszéspontot mindig \(\displaystyle 1{,}8\) egységgel előzzük meg. (Az ábra \(\displaystyle n=4\) esetén mutatja a két spirált.) Milyen \(\displaystyle n\) érték mellett lesz a két spirál hossza megegyező?
(5 pont)
A beküldési határidő 2015. október 12-én LEJÁRT.
Megoldás. Az \(\displaystyle n\) egység oldalú négyzetből készült spirál ,,oldalainak" hossza belülről kifelé haladva sorban \(\displaystyle 1,\, 1,\, 2,\, 2,\, 3,\, 3,\, \dots,\, n-1,\, n-1,\, n,\, n,\, n\). Ezek összege: \(\displaystyle 2\cdot(1+2+\dots+n)+n=2\cdot\frac{(1+n)n}{2}+n=n^2+2n\).
Az \(\displaystyle 1{,}8n\) egység oldalú szabályos háromszögből készült spirál oldalainak hossza pedig rendre \(\displaystyle 1,8;\, 2\cdot1,8;\, 3\cdot1,8;\, \dots;\, (n-1)\cdot1,8;\, n\cdot1,8;\, n\cdot1,8\). Ezek összege: \(\displaystyle 1,8(1+2+\dots+n)+1,8n=1,8\cdot\frac{n(n+1)}{2}+1,8n=0,9n^2+0,9n+1,8n\).
Ha a kettő egyenlő:
\(\displaystyle n^2+2n=0,9n^2+0,9n+1,8n,\)
amiből
\(\displaystyle 0,1^2-0,7n=0.\)
Ezt 10-zel szorozva, majd szorzattá bontva:
\(\displaystyle n^2-7n=n(n-7)=0.\)
Ennek egyetlen pozitív megoldása az \(\displaystyle n=7\).
Tehát \(\displaystyle n=7\) esetén lesz a két sprirál hossza megegyező.
Statisztika:
250 dolgozat érkezett. 5 pontot kapott: 102 versenyző. 4 pontot kapott: 61 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 58 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2015. szeptemberi matematika feladatai
