 |
A C. 1327. feladat (2015. december) |
C. 1327. Hogyan tudjuk az ábrán látható tulajdonságokkal rendelkező nyolcszöget egy belső pontjából induló szakaszokkal négy részre darabolni úgy, hogy a kapott részekből két, egybevágó szabályos ötszöget rakhassunk össze?
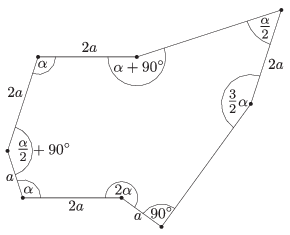
(5 pont)
A beküldési határidő 2016. január 11-én LEJÁRT.
Megoldás. Mivel egy nyolcszög belső szögeinek összege \(\displaystyle 6\cdot180^{\circ}=1080^{\circ}\) és az első ábrán a szögek összege \(\displaystyle 7,5\alpha+270^{\circ}\), így \(\displaystyle 1080^{\circ}=7,5\alpha+270^{\circ}\), amiből \(\displaystyle \alpha =108{}^{\circ}\). Ez éppen a szabályos ötszög egy belső szögének nagysága.

1. ábra
Ebből sejthető, hogy az ötszögek oldalai \(\displaystyle 2a\) hosszúak lesznek. Az \(\displaystyle A\) csúcsban \(\displaystyle \frac{\alpha } 2+90{}^{\circ}\) található, így ezt érdemes lehet úgy kettébontani, hogy egy \(\displaystyle \alpha /2\) nagyságú és egy \(\displaystyle 90{}^{\circ}\)-os szöget kapjunk. A \(\displaystyle C\) csúcsnál pedig egy \(\displaystyle \alpha \) és egy \(\displaystyle 90{}^{\circ}\) -os szögre érdemes bontani. Jelölje \(\displaystyle P\) az \(\displaystyle A\) csúcsban az \(\displaystyle AH\) oldalra állított merőleges és a \(\displaystyle C\) csúcsban a \(\displaystyle CD\) oldalra állított merőleges metszéspontját. Az \(\displaystyle APCB\) négyszöget tükrözve az \(\displaystyle AP\) oldalra egy szabályos ötszöget kapunk, hiszen négy oldala egyenlő és minden szöge \(\displaystyle 108^{\circ}\). Legyen \(\displaystyle \overline{AP}=b\).
Helyezzünk el négy ilyen négyszöget a 2. ábrának megfelelően. Ekkor a négy négyszögből összerakható két szabályos ötszög.

2. ábra
Látható, hogy az I és a II, a II és a III, a III és a IV, valamint a IV és az I négyszögek egyenlő hosszúságú oldalai érintkeznek egymással, a kapott nyolcszög szögei épp az adott szögek lesznek, illetve a \(\displaystyle P\) pontnál összesen \(\displaystyle 360^{\circ}\) jön létre a négy négyszögből együttesen. Vagyis éppen az adott hatszöget kaptuk.
Tehát a \(\displaystyle P\) csúcsot összekötve a hatszög megfelelő két másik csúcsával, egy jó felbontást kapunk.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Bánóczi Anna, Bőzsöny András, Csapó Márton, Csorba Benjámin, Fülöp Ágota, Gera Dóra, Horeftos Leon, Horváth András János, Inges Zénó, Kasó Ferenc, Kocsis Júlia, Kormányos Hanna Rebeka, Kósa Szilárd, Matusek Márton, Mészáros 01 Viktória, Nagy 911 Viktória, Souly Alexandra, Sudár Ákos, Szabó Alexandra, Tar Viktor, Tatai Mihály, Tóth Adrián, Ványi Virág. 4 pontot kapott: Horváth Tibor 1998, Kiss Vivien Mercédesz, Komoróczy Ádám, Kovács Iván, Sándor 158 Alexandra. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2015. decemberi matematika feladatai
