 |
A C. 1695. feladat (2021. december) |
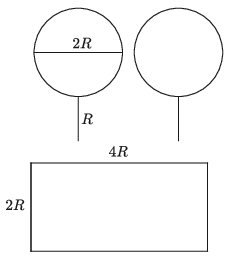
C. 1695. Egy körvonalhoz rá merőlegesen hozzárögzítünk egy sugárnyi \(\displaystyle (R)\) hosszúságú szakaszt (lásd az ábrát). Belefér-e két, ilyen szakasszal ellátott kör (,,serpenyő'') egy olyan téglalapba, aminek az egyik oldala a kör átmérője (\(\displaystyle 2R\)), a másik pedig kétszer akkora (\(\displaystyle 4R\))? Az alakzatok és a téglalap érinthetik, de nem metszhetik és nem fedhetik egymást.
Javasolta: Gáspár Merse Előd (Budapest)
(5 pont)
A beküldési határidő 2022. január 10-én LEJÁRT.
1. Megoldás. Legyen a körök sugara \(\displaystyle R=1\), ezzel a körök átmérője \(\displaystyle 2\) egységnyi, a téglalap oldalai pedig \(\displaystyle 2\), illetve \(\displaystyle 4\) egységnyi hosszúságúak. Ha csak a köröket kell elhelyezni a téglalapban, akkor azok nyilvánvalóan elférnek benne, mégpedig egyféleképpen, úgy, hogy mindkettő érinti a téglalap három oldalát, és a két kör érinti is egymást.
A kérdés az, hogy a körhöz rögzített egységnyi szakaszok beférnek-e a téglalapba. Bizonyítani fogjuk, hogy akkor férnek el, ha az egyik körhöz rögzített szakasz érinti a másik kört, és megfordítva. Tekintsük a következő ábrát, amelyen a körök \(\displaystyle A\), illetve \(\displaystyle B\) középpontjaiból érintőket rajzoltunk a másik körhöz, így kaptuk az \(\displaystyle AH\), illetve \(\displaystyle BE\) érintőszakaszokat. Az \(\displaystyle AH\) félegyenes a téglalap \(\displaystyle 4\) egységnyi oldalát a \(\displaystyle K\) pontban, a \(\displaystyle BE\) félegyenes pedig a téglalap előzővel szemben levő oldalát az \(\displaystyle F\) pontban metszi. A körök egymást a \(\displaystyle C\) pontban, a téglalap egy-egy oldalát a \(\displaystyle G\), illetve \(\displaystyle L\) pontban érintik az ábra szerint.

Azt fogjuk igazolni, hogy \(\displaystyle BF=2\).
Ehhez megrajzoltuk az \(\displaystyle AB\)-re merőleges \(\displaystyle FM\) szakaszt. Nyilvánvaló, hogy \(\displaystyle AC=BC=AG=AE=BH=BL=1\), de mivel \(\displaystyle AMFG\) téglalap, ezért \(\displaystyle FM=1\) is igaz.
Az \(\displaystyle ABE\) derékszögű háromszögben az \(\displaystyle AB\) átfogó hossza \(\displaystyle AB=AC+BC=2\), illetve \(\displaystyle AE=1\), ezért ez a háromszög egy szabályos háromszög fele, így \(\displaystyle ABE\sphericalangle=30^{\circ}\) és \(\displaystyle BAE\sphericalangle=60^{\circ}\).
Emiatt a \(\displaystyle BFM\) derékszögű háromszögben \(\displaystyle MBF\sphericalangle=30^{\circ}\), ezért \(\displaystyle MFB\sphericalangle=60^{\circ}\), és mivel az egységnyi hosszú \(\displaystyle FM\) a rövidebbik befogó, ezért ezen befogó hosszának kétszerese a \(\displaystyle BF\) átfogó. Ez éppen azt jelenti, hogy \(\displaystyle BF=2\) valóban teljesül.
Ha pedig ez igaz, akkor mivel \(\displaystyle BD=1\), azért \(\displaystyle DF=1\) is fennáll, eszerint a \(\displaystyle B\) középpontú körhöz rögzített egységnyi hosszú \(\displaystyle DF\) szakasz, érintve az \(\displaystyle A\) középpontú kört, a feltételeknek megfelelően éppen elfér a téglalap belsejében.
Hasonlóan egyszerűen igazolhatjuk, hogy \(\displaystyle AK=2\) is igaz, tehát az \(\displaystyle A\) középpontú körhöz rögzített egységnyi hosszú \(\displaystyle NK\) szakasz is éppen elfér a téglalap belsejében.
2. Megoldás. Legyen \(\displaystyle R=1\) és használjuk az 1. megoldás ábráját, azzal a kiegészítéssel, hogy az \(\displaystyle FG\) szakaszt \(\displaystyle x\)-szel jelöljük.
Most is azt fogjuk igazolni, hogy \(\displaystyle BF=2\).
Az \(\displaystyle A\) középpontú körhöz húzott érintőszakaszok hosszának egyenlősége miatt \(\displaystyle FG=FE=x\), ezért \(\displaystyle BF=BE+x\). Mivel \(\displaystyle AE=1\) és \(\displaystyle AB=2\), ezért az \(\displaystyle ABE\) olyan derékszögű háromszög, amelyben a \(\displaystyle BE\) szakasz hossza a Pitagorasz-tétel alkalmazásával \(\displaystyle BE=\sqrt{3}\).
Az \(\displaystyle ABE\) háromszög egy szabályos háromszög fele, tehát \(\displaystyle ABE\sphericalangle=30^{\circ}\) és \(\displaystyle BAE\sphericalangle=60^{\circ}\).
Az \(\displaystyle AFG\) és \(\displaystyle AEG\) derékszögű háromszögek egybevágók, mert az \(\displaystyle AF\) átfogójuk közös, befogóik pedig egyenlő hosszúak, hiszen \(\displaystyle AG=AE=1\) és \(\displaystyle FG=FE=x\), a két háromszög megfelelő szögei ezért egyenlők. Ebből \(\displaystyle BAE\sphericalangle=60^{\circ}\) alapján az következik, hogy \(\displaystyle GAF\sphericalangle=EAF\sphericalangle=15^{\circ}\), és így \(\displaystyle \tg15^{\circ}=\frac{FE}{AE}=\frac{x}{1}\), azaz
| \(\displaystyle (1)\) | \(\displaystyle FE=x=\tg15^{\circ}.\) |
A \(\displaystyle \tg(\alpha-\beta)=\frac{\tg{\alpha}-\tg{\beta}}{1+\tg{\alpha}\cdot{\tg{\beta}}}\) trigonometrikus azonosságot alkalmazhatjuk az \(\displaystyle \alpha=45^{\circ}\) és \(\displaystyle \beta=30^{\circ}\) szögekre, és felhasználhatjuk, hogy \(\displaystyle \tg45^{\circ}=1\), illetve \(\displaystyle \tg30^{\circ}=\frac{\sqrt{3}}{3}\). A műveletek elvégzésével, egyszerűsítéssel és a törtkifejezés nevezőjének négyzetgyöktelenítésvel azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \tg15^{\circ}=2-\sqrt{3}.\) |
Az (1) és (2) egyenlőségek figyelembe vételével adódik, hogy \(\displaystyle FE=2-\sqrt{3}\). Mivel \(\displaystyle BF=BE+FE\) és \(\displaystyle BE=\sqrt{3}\), ezért \(\displaystyle BF=\sqrt{3}+2-\sqrt{3}\), vagyis \(\displaystyle BF=2\). Ez éppen azt jelenti, hogy a \(\displaystyle B\) középpontú körhöz rögzített \(\displaystyle DF\) szakasz hossza egységnyi, tehát a \(\displaystyle DF\) szakasz, érintve az \(\displaystyle A\) középpontú kört, éppen elfér a téglalap belsejében.
Hasonlóan egyszerűen igazolhatjuk, hogy \(\displaystyle AK=2\) is fennáll, ezért az \(\displaystyle A\) középpontú körhöz rögzített egységnyi hosszú \(\displaystyle NK\) szakasz is éppen elfér a téglalap belsejében.
Megjegyzés. A \(\displaystyle \tg15^{\circ}\) pontos értékéhez a trigonometrikus azonosság alkalmazása nélkül is eljuthatunk. Kiszámíthatjuk a belső szögfelezőre vonatkozó tétel alapján, hogy az \(\displaystyle 1;\sqrt{3};2\) oldalú derékszögű háromszögben az \(\displaystyle 1\) egységnyi befogót a szemközti, \(\displaystyle 30^{\circ}\)-os szög felezője egy \(\displaystyle \frac{\sqrt{3}}{\sqrt{3}+2}\) és egy \(\displaystyle \frac{2}{\sqrt{3}+2}\) hosszúságú szakaszra osztja. Ezek közül a \(\displaystyle \frac{\sqrt{3}}{\sqrt{3}+2}\) hosszúságú egy olyan derékszögű háromszög befogója, amelyben a befogóval szemközti szög \(\displaystyle 15^{\circ}\)-os, és a háromszög másik befogójának hossza \(\displaystyle \sqrt{3}\). Így \(\displaystyle \tg15^{\circ}=\frac{\frac{\sqrt{3}}{\sqrt{3}+2}}{\sqrt{3}}=\frac{1}{\sqrt{3}+2}\), a nevező négyzetgyöktelenítése után pedig \(\displaystyle \tg15^{\circ}=2-\sqrt{3}\).
Statisztika:
A KöMaL 2021. decemberi matematika feladatai
