 |
A C. 1782. feladat (2023. október) |
C. 1782. Az \(\displaystyle ABCD\) négyzet \(\displaystyle D\) csúcsából érintőt húzunk az \(\displaystyle AB\) átmérőjű, a négyzet belsejébe rajzolt félkörhöz, az érintési pont (az \(\displaystyle A\)-tól különböző) \(\displaystyle E\) pont, az \(\displaystyle AB\) szakasz felezőpontja \(\displaystyle F\). Az érintő a \(\displaystyle BC\) egyenest a \(\displaystyle G\), az \(\displaystyle AB\) egyenest a \(\displaystyle H\), valamint az \(\displaystyle EF\) egyenes a \(\displaystyle DA\) egyenest a \(\displaystyle K\) pontban metszi. Bizonyítsuk be, hogy az \(\displaystyle FHE\), \(\displaystyle DGC\) és \(\displaystyle DKE\) háromszögek beírt köreinek sugarai ebben a sorrendben egy növekvő számtani sorozat közvetlen egymás utáni tagjai.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. november 10-én LEJÁRT.
I. megoldás A megoldás során fel fogjuk használni azt az ismert összefüggést, hogy ha egy derékszögű háromszög befogói \(\displaystyle a\) és \(\displaystyle b\), átfogója \(\displaystyle c\), akkor beírt körének sugara
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{r=\frac{a+b-c}{2}}.\) |
Tekintsük a következő ábrát, amelyen a négyzet oldalának hosszát \(\displaystyle a\)-val jelöltük.
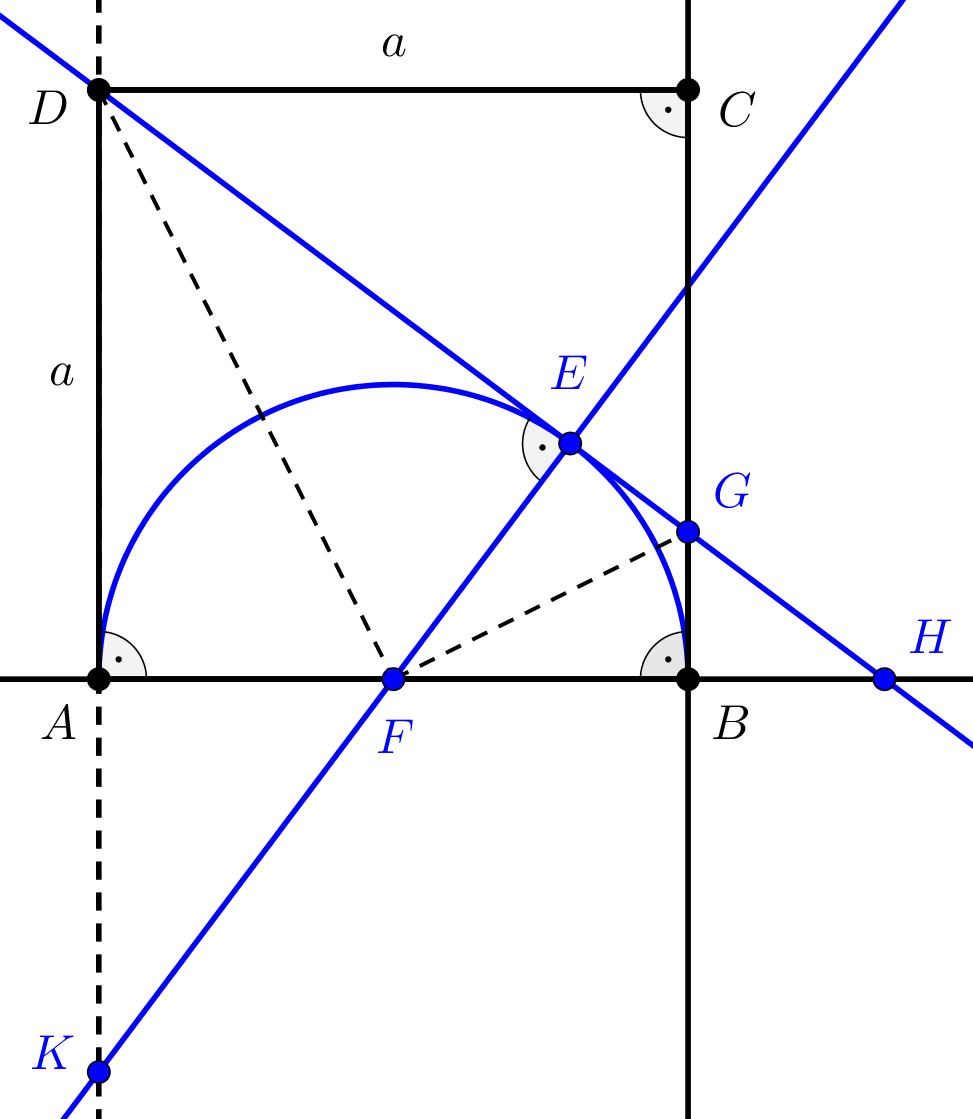
A \(\displaystyle DE\) érintő merőleges a félkör középpontjából az érintési pontba húzott sugárra, ezért \(\displaystyle DE\perp FE\), vagyis az \(\displaystyle FHE\), \(\displaystyle DGC\) és \(\displaystyle DKE\) háromszögek mindegyike derékszögű. Másrészt pedig \(\displaystyle \displaystyle{FA=FB=FE=\frac{a}{2}}\) és az érintőszakaszok hosszának egyenlősége miatt \(\displaystyle DA=DE=a\).
Ezek alapján kiszámítjuk az \(\displaystyle FHE\), \(\displaystyle DGC\), \(\displaystyle DKE\) derékszögű háromszögek oldalainak hosszát.
Az \(\displaystyle FDA\) és \(\displaystyle FDE\) derékszögű háromszögek a megfelelő oldalak hosszának egyenlősége miatt egybevágók. A \(\displaystyle GE\) és \(\displaystyle GB\) a félkörhöz húzott érintőszakaszok, az \(\displaystyle FGE\) és \(\displaystyle FGB\) derékszögű háromszögek megfelelő oldalainak hossza is egyenlő, tehát ezek a háromszögek is egybevágók. Az egybevágó háromszögek megfelelő szögei egyenlők, így \(\displaystyle FD\) felezi az \(\displaystyle AFE \sphericalangle\)-et, \(\displaystyle FG\) pedig felezi a \(\displaystyle BFE \sphericalangle\)-et. Ezt azt jelenti, hogy \(\displaystyle DFG\sphericalangle=90^{\circ}\). A \(\displaystyle DGF\) derékszögű háromszögben alkalmazhatjuk a magasságtételt, eszerint \(\displaystyle FE=\sqrt{DE\cdot GE}\), azaz \(\displaystyle \displaystyle{\frac{a}{2}=\sqrt{a\cdot GE}}\), ahonnan a műveletek elvégzésével és egyszerűsítéssel kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{GE=GB=\frac{a}{4}}.\) |
A \(\displaystyle HGB\) és \(\displaystyle HDA\) derékszögű háromszögek megfelelő szögei egyenlők, ezért a két háromszög hasonló, a hasonlóság aránya (2) alapján \(\displaystyle \displaystyle{\frac{1}{4}}\), így
\(\displaystyle \displaystyle{\frac{BH}{BH+a}=\frac{1}{4}},\)
ebből egyszerű számolással adódik, hogy
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{BH=\frac{a}{3}},\) |
innen pedig (például a \(\displaystyle HGB\) háromszögre felírt Pitagorasz-tétel segítségével) kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{HG=\frac{5a}{12}}.\) |
Az \(\displaystyle FHE\) derékszögű háromszög befogói és átfogója tehát a (2)–(3)–(4) összefüggések segítségével:
\(\displaystyle \displaystyle{FE=\frac{a}{2}=\frac{6a}{12}; \qquad EH=GE+HG=\frac{a}{4}+\frac{5a}{12}=\frac{8a}{12};\qquad FH=FB+BH=\frac{a}{2}+\frac{a}{3}=\frac{10a}{12}}.\)
Alkalmazzuk az (1) tételt az \(\displaystyle FHE\) derékszögű háromszögre, ahonnan egyszerű számolás után:
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{r_{FHE}=\frac{2a}{12}}.\) |
Felhasználjuk (2)-t és azt, hogy \(\displaystyle DE=a\), ezzel a \(\displaystyle DGC\) derékszögű háromszög befogóinak és átfogójának hossza:
\(\displaystyle \displaystyle{CD=a=\frac{12a}{12}; \qquad CG=a-GB=\frac{3a}{4}=\frac{9a}{12};\qquad DG=DE+GE=a+\frac{a}{4}=\frac{15a}{12}},\)
ezek alapján az (1) tételből
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{r_{DGC}=\frac{3a}{12}}\) |
következik.
Az \(\displaystyle FKA\) és \(\displaystyle FHE\) derékszögű háromszögek közös \(\displaystyle F\) csúcsánál levő belső szögei csúcsszögek, tehát egyenlő nagyságúak, ezért a két háromszög másik hegyesszöge is egyenlő, így a háromszögek hasonlók, de mivel a megfelelő \(\displaystyle FA\) és \(\displaystyle FE\) befogók hossza egyaránt \(\displaystyle \displaystyle{\frac{a}{2}}\), ezért a két háromszög egybevágó. Ez azt jelenti, hogy
\(\displaystyle \displaystyle{AK=EH=\frac{8a}{12}};\qquad FK=FH=\frac{10a}{12},\)
ezért a \(\displaystyle DKE\) derékszögű háromszög befogói és átfogója:
\(\displaystyle \displaystyle{DE=a=\frac{12a}{12}; \qquad KE=\frac{a}{2}+FK=\frac{16a}{12};\qquad DK=a+AK=\frac{20a}{12}},\)
így tehát (1) szerint
| \(\displaystyle (7)\) | \(\displaystyle \displaystyle{r_{DKE}=\frac{4a}{12}}.\) |
Az (5)–(6)–(7) egyenlőségek igazolják a feladat állítását, amely szerint az \(\displaystyle FHE\), \(\displaystyle DGC\) és \(\displaystyle DKE\) háromszögek beírt köreinek sugarai ebben a sorrendben egy növekvő számtani sorozat közvetlen egymás utáni tagjai, a számtani sorozat különbsége pontosan a négyzet oldalhosszának \(\displaystyle \displaystyle{12}\)-ed része. Ezzel a megoldást befejeztük.
II. megoldás Használjuk az I. megoldás-hoz készített ábrát. Megállapításaink a (2)-vel jelzett összefüggésig megegyeznek az előző megoldással.
Legyen most \(\displaystyle ADE\sphericalangle=\alpha\), ekkor könnyen látható, hogy \(\displaystyle FHE\sphericalangle=EDC\sphericalangle=DKE\sphericalangle=90^{\circ}-\alpha\), továbbá \(\displaystyle DGC\sphericalangle=HFE\sphericalangle=\alpha\).
Mindezekből az következik, hogy az alábbi derékszögű háromszögek páronként hasonlók:
\(\displaystyle FHE \sim GDC \sim DKE.\)
Jelöljük az \(\displaystyle FHE\) beírt körének sugarát \(\displaystyle r\)-rel.
Ekkor az \(\displaystyle FHE\)-t a \(\displaystyle GDC\)-be képező hasonlóság aránya alapján megkaphatjuk a \(\displaystyle GDC\) beírt körének sugarát. Az arány a két derékszögű háromszög megfelelő oldalainak arányával, ebben az esetben a \(\displaystyle 90^{\circ}-\alpha\) szöggel szemközti befogók arányával egyenlő:
\(\displaystyle \displaystyle{\frac{CG}{FE}=\frac{a-\frac{1}{4}a}{\frac{a}{2}}=\frac{\frac{3}{4}a}{\frac{a}{2}}=\frac{3}{2}}.\)
Ezért a \(\displaystyle GDC\) háromszög beírt körének sugara \(\displaystyle \displaystyle{\frac{3}{2}r}\).
Hasonlóképpen belátható, hogy a \(\displaystyle GDC\) háromszöget a \(\displaystyle DKE\) háromszögbe képező hasonlóság aránya
\(\displaystyle \displaystyle{\frac{CG}{DE}=\frac{a}{\frac{3}{4}a}=\frac{4}{3}},\)
így a \(\displaystyle DKE\) beírt körének sugara a \(\displaystyle GDC\)-be írt kör sugarának \(\displaystyle \displaystyle{\frac{4}{3}}\)-a, vagyis \(\displaystyle \displaystyle{\frac{3}{2}r\cdot \frac{4}{3}=2r}\).
A három sugár tehát rendre
\(\displaystyle \displaystyle{r,\qquad \frac{3}{2}r,\qquad 2r}.\)
Ezek valóban egy számtani sorozat egymást követő tagjai.
Megjegyzés. Könnyen belátható, hogy a II. megoldás-ban kapott \(\displaystyle \displaystyle{d=\frac{r}{2}}\) érték az \(\displaystyle ABCD\) négyzet oldalhosszának \(\displaystyle 12\)-ed része, azaz \(\displaystyle \displaystyle{\frac{r}{2}=\frac{a}{12}}\), és ezért \(\displaystyle \displaystyle{r=\frac{a}{6}}\).
Statisztika:
65 dolgozat érkezett. 5 pontot kapott: Baksa Anna, Baumgartner Ádám, Bencze Mátyás, Braun Zsófia, Dancsák Dénes, Fiser 234 Boldizsár, Gál András, Gombos Dániel , Gyuricsek Ákos, Han Xinzhi, Inokai Ádám, Iván Máté Domonkos, Járdánházi-Kurutz Vilmos, Márfai Dóra, Masa Barnabás, Medgyesi Júlia, Nagy 292 Korina, Németh Hanna Júlia , Seprődi Barnabás Bendegúz, Szabó Donát, Telkes Ágota, Török Eszter Júlia, Volford Barnabás, Žigo Boglárka. 4 pontot kapott: Alexandrova Angelina, Balogh Péter, Barna Márton, Bérczes Botond, Bettesch Emma Léda, Ehrlich Máté, Károlyi József, Papp Zsófia, Petró Péter, Simon Bálint. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2023. októberi matematika feladatai
