A C. 804. feladat (2005. március)

C. 804. Egy mértani sorozat első eleme 6, az első n elem összege 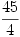$\frac{45}{4}$ , ugyanezen elemek reciprokainak összege 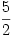$\frac{5}{2}$ . Melyik ez a mértani sorozat?

(5 pont)

A beküldési határidő 2005. április 15-én LEJÁRT.

Megoldás. A mértani sorozat első eleme a₁=6. A sorozat hányadosa nem lehet 1, hiszen akkor az első n elemének összege: ${45\over4}=6n$ , azaz $n={45\over24}$ lenne, ami nem egész. Az ismert képlet szerint: $S_n=a_1{q^n-1\over q-1}$ , azaz

$6{q^n-1\over q-1}={45\over4}.$

Rendezzük az egyenletet:

(1)	$q^n-1={15\over8}(q-1).$

A reciprok sorozatra:

${1\over6}{({1\over q})^n-1\over{1\over q}-1}={5\over2}.$

Végezzük el a kijelölt műveleteket. Rendezés után kapjuk, hogy

(2)	qⁿ-1=15(qⁿ-q^n-1).

Helyettesítsük (2)-be az (1)-ből (qⁿ-1)-re kapott kifejezést:

${15\over8}(q-1)=15(q^n-q^{n-1})=15q^{n-1}(q-1).$

Osztva a 15(q-1) $\neq$ 0-val: ${1\over8}=q^{n-1}$ , innen $q^n={1\over8}q$ . Ezt (1)-be beírva kapjuk, hogy ${1\over8}q-1={15\over8}(q-1)$ , ahonnan $q={1\over2}$ és $({1\over2})^n={1\over16}$ -ból n=4.

Az első sorozat elemei: 6, 3, ${3\over2}$ és ${3\over4}$ ; ezek összege valóban ${45\over4}$ .

A második sorozat elemei: ${1\over6}$ , ${1\over3}$ , ${2\over3}$ és ${4\over3}$ és ${1\over6}+{1\over3}+{2\over3}+{4\over3}={15\over6}={5\over2}.$

Statisztika:

171 dolgozat érkezett.

5 pontot kapott: 62 versenyző.

4 pontot kapott: 65 versenyző.

3 pontot kapott: 30 versenyző.

2 pontot kapott: 3 versenyző.

1 pontot kapott: 3 versenyző.

0 pontot kapott: 6 versenyző.

Nem versenyszerű: 2 dolgozat.

A KöMaL 2005. márciusi matematika feladatai

171 dolgozat érkezett.
5 pontot kapott:	62 versenyző.
4 pontot kapott:	65 versenyző.
3 pontot kapott:	30 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	2 dolgozat.

Már regisztráltál?
Új vendég vagy?