Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 812. feladat (2005. május)

C. 812. Megy a gőzös Kanizsára a 21 km távolságra lévő Zalakomárról. Az utat 16 perc alatt teszi meg úgy, hogy indulástól egyenletesen gyorsul, majd 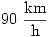90~\frac{\rm km}{\rm h} állandó sebességgel halad, végül egyenletesen lassulva megáll. Mennyi ideig megy a gőzös 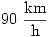90~\frac{\rm km}{\rm h} sebességgel?

(5 pont)

A beküldési határidő 2005. június 15-én LEJÁRT.

Megoldás. A vonat mozgását sebesség-idő koordináta-rendszerben ábrázoljuk, km/perc, ill. perc mértékegységgel számolva.

Az indulástól számítva az egyenletes gyorsulás idejét a-val, az egyenletes sebességgel való haladásét x-szel, végül a lassulás idejét b-vel jelöljük. Ekkor a+x+b=16, és a megtett 21 km út a mozgást leíró függvénygörbe és az abszcissza által bezárt síkidom - egy trapéz - területével egyenlő. Tehát

21=((a+x+b)+x).1.5/2=(16+x).1.5/2,

ahonnan x=12 perc a 90 \dfrac{\text{km}}{\text{h}} sebességgel történt haladás ideje.

Statisztika:

153 dolgozat érkezett.
5 pontot kapott:146 versenyző.
4 pontot kapott:1 versenyző.
3 pontot kapott:1 versenyző.
2 pontot kapott:1 versenyző.
1 pontot kapott:2 versenyző.
0 pontot kapott:2 versenyző.

A KöMaL 2005. májusi matematika feladatai