Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 889. feladat (2007. február)

C. 889. Az ábrán felülnézetben látható csonkagúla alaplapjai téglalapok, magassága m. Valaki a csonkagúla térfogatára a következő képletet találta:

V= \frac{m}{6} \big[(2a+c)b+ (2c+a)d\big].

Igaz-e, hogy a képlet megadja a test térfogatát?

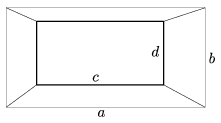
(5 pont)

A beküldési határidő 2007. március 19-én LEJÁRT.

Megoldás. A csonkagúla térfogatképlete szerint a térfogat:

(1)V_{\rm csg}=\frac{m}{3}\left(ab+\sqrt{abcd}+cd\right).

A megadott képlet szerint a térfogat:

V=\frac{m}{6}\left[(2a+c)b+(2c+a)d\right]=

(2)\frac{m}{3}\left(ab+\frac{bc}{2}+cd+\frac{ad}{2}\right).

(1) és (2) pontosan akkor egyenlők, ha

(3)\sqrt{abcd}=\frac{bc}{2}+\frac{ad}{2}.

Mivel a test csonkagúla, ezért alaplapjai hasonlóak, és így d/b=c/a, vagyis ad=bc. Ezt felhasználva (3) így alakul:

\sqrt{ ad\cdot ad}=\frac{ad}{2}+\frac{ad}{2},

ad=ad.

A képlet a test térfogatát adja.

Statisztika:

301 dolgozat érkezett.
5 pontot kapott:106 versenyző.
4 pontot kapott:91 versenyző.
3 pontot kapott:66 versenyző.
2 pontot kapott:23 versenyző.
1 pontot kapott:7 versenyző.
0 pontot kapott:8 versenyző.

A KöMaL 2007. februári matematika feladatai