 |
A C. 968. feladat (2008. december) |
C. 968. Az ABCD négyzetet az ábrán látható módon az oldalaival párhuzamos egyenesekkel az NPLD és KBMP négyzetekre és két egybevágó téglalapra osztottuk.
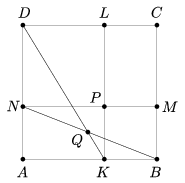
Legyen KL és MN metszéspontja P, BN és DK metszéspontja pedig Q. Mutassuk meg, hogy a C, P és Q pontok egy egyenesre illeszkednek.
(5 pont)
A beküldési határidő 2009. január 15-én LEJÁRT.
Megoldás. Három pár egybevágó téglalappárt látunk az ábrán, amelyek egymás 90o-os elforgatottjai: MCDN és LDAK, KBCL és BMNA, valamint PMCL és KPNA. Ezért a megfelelő átlók merőlegesek egymásra. Vagyis ,
. Ezért a KCN háromszögben Q magasságpont. Mivel
, ezért a PC egyenes a harmadik magasság, vagyis átmegy a Q ponton. Azaz a C, P és Q pontok valóban egy egyenesre illeszkednek.
Statisztika:
129 dolgozat érkezett. 5 pontot kapott: 89 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 28 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2008. decemberi matematika feladatai
