Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 976. feladat (2009. február)

C. 976. Adjuk meg azt a legszűkebb intervallumot, ahová három pozitív szám összegének és a reciprokaik összegének szorzata eshet.

(5 pont)

A beküldési határidő 2009. március 16-án LEJÁRT.

Megoldás. Néhány számhármas kipróbálása utáni sejtésünk:

(a+b+c)\left(\frac 1a+\frac 1b+\frac 1c\right)\geq9.

Beszorzás után kapjuk, hogy:

1+\frac ab+\frac ac+\frac ba+1+\frac bc+\frac ca+\frac cb+1\geq9.

A tagokat átcsoportosítva:

3+\left(\frac ab+\frac ba\right)+\left(\frac ac+\frac ca\right)+\left(\frac bc+\frac cb\right)\geq9.

Egy pozitív szám és reciprokának összege legalább 2, tehát az egyenlőtlenség igaz.

A szorzat pedig bármilyen n egész számnál nagyobb lehet, hiszen ehhez elég, ha például a=nb teljesül.

Vagyis a legszűkebb intervallum, ahova a szorzat eshet: [9;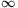\infty[.

Statisztika:

192 dolgozat érkezett.
5 pontot kapott:74 versenyző.
4 pontot kapott:46 versenyző.
3 pontot kapott:45 versenyző.
2 pontot kapott:13 versenyző.
1 pontot kapott:5 versenyző.
0 pontot kapott:5 versenyző.
Nem versenyszerű:4 dolgozat.

A KöMaL 2009. februári matematika feladatai