A G. 739. feladat (2021. március)

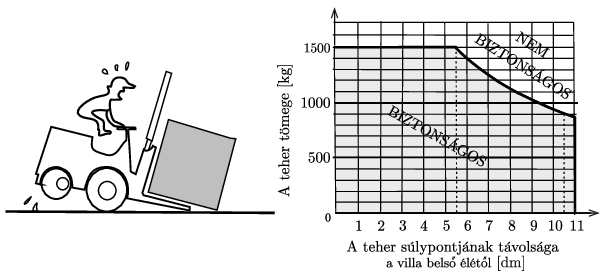
G. 739. A nem megfelelően elhelyezett terhek felboríthatják a villástargoncát. Ezért a targoncákhoz mellékelnek egy úgynevezett villaterhelési diagramot (lásd az ábrát). Állapítsuk meg a diagram alapján, hogy milyen vízszintes távolságra van a villa sarokpontjától a targonca első kerekének tengelye, illetve, hogy vízszintes irányban milyen messze van a villa sarkától az 1200 kg-os targonca súlypontja!

(4 pont)

A beküldési határidő 2021. április 15-én LEJÁRT.

I. megoldás. Ha túl nehéz a teher, a targonca az első kerekei körül elfordulva felbillenhet. A felbillenés határesetében az első kerekekre vonatkoztatott forgatónyomatékok éppen egyensúlyban vannak. Ennek feltétele (a bal oldali ábra jelöléseivel):

(A targonca súlyához nem számítottuk hozzá a vezető súlyát, hiszen ő le is szállhat a járművéről, és a biztonságot nyilván nem szabad ilyen esetleges helyzetektől függővé tenni. A villaterhelési diagram tehát a kezelő nélküli viszonyokra vonatkozik.)

A diagramon a BIZTONSÁGOS tartomány jobb széle azt jelzi, hogy a teher a villa vége körül is lebillenhet, a tartomány felső határvonala pedig a targonca teherbíróképességére utal. A tartomány ,,íves'' határvonala az (1) egyenletnek felel meg. A \(\displaystyle G(x)\) függvény két ismeretlen adatot (paramétert) tartalmaz, ezeket szeretnénk a függvény grafikonja alapján meghatározni. Ábrázoljuk a

\(\displaystyle \frac{G_0}{G}=\frac{x+d}{\ell-d}\)

lineáris függvényt a feladatban megadott grafikon alapján. (A súlyok aránya helyett számolhatunk a kg-ban megadott tömegek arányával.) Néhány pont felvétele után megrajzolhatjuk a lineáris függvénynek megfelelő egyenest (ld. az ábra jobb oldali részét). A grafikonról leolvasható, hogy a \(\displaystyle G_0/G=0\) tengelymetszetnél \(\displaystyle \vert x\vert=d=2~\)dm, a targonca első tengelye tehát 2 dm távol van a villa sarkától.

A grafikonról az is leolvasható, hogy az egyenes meredeksége:

\(\displaystyle m=\frac{1}{\ell-d}\approx \frac{1{,}38}{13~\rm dm}=0{,}106~\rm dm^{-1}.\)

Innen \(\displaystyle d\) már meghatározott értékének felhasználásával az \(\displaystyle \ell\approx 11{,}4~\rm dm\) eredmény adódik. A targonca súlyvonala tehát kb. \(\displaystyle 11{,}4~\rm dm\) távolságban van a villa sarokvonalától.

II. megoldás. Az I. megoldás jelöléseit és gondolatmenetét követve az (1) egyenletből függvényillesztés nélkül is meghatározhatjuk az \(\displaystyle \ell\) és \(\displaystyle d\) paramétereket. A feladathoz tartozó grafikonon szaggatott vonallal jelölt pontok helyzetéből leolvasható, hogy \(\displaystyle x=5{,}5~\rm dm\)-nél a legnagyobb megengedett teher tömege 1500 kg, \(\displaystyle x=10{,}5\) dm-nél pedig 900 kg. Felírhatjuk tehát (kg és dm egységekkel számolva) az

\(\displaystyle 1500\,(5{,}5+d)=1200\,(\ell-d),\)

\(\displaystyle 900\,(10{,}5+d)=1200\,(\ell-d) \)

egyenletrendszert, amelynek megoldása: \(\displaystyle d=\)2 dm és \(\displaystyle \ell= 11{,}375~{\rm dm}\approx 11{,}4~{\rm dm}\).

Statisztika:

28 dolgozat érkezett.
4 pontot kapott:	Beke Botond, Bencz Benedek, Bogdán Benedek, Bruder László, Buzási-Temesi Imre, Cynolter Dorottya, Czirók Tamás, Fehérvári Donát, Hegedűs Máté Miklós, Jeszenői Sára, Josepovits Gábor, Kovács Dorina , Lipóczi Levente, Marozsi Lenke Sára, Molnár Kristóf, Richlik Márton, Sebestyén József Tas, Vágó Botond, Veszprémi Rebeka Barbara, Vig Zsófia, Vincze Farkas Csongor, Waldhauser Miklós, Wórum Soma.
3 pontot kapott:	Dancsák Dénes, Láng Erik, Novák Péter, Patricia Janecsko, Stein Felix.

A KöMaL 2021. márciusi fizika feladatai