A G. 744. feladat (2021. április)

G. 744. Az ábrán látható áramkör négy egyforma, \(\displaystyle 10~\Omega\)-os ellenállásból és egy telepből áll.

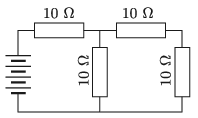
\(\displaystyle a)\) Mekkora a telep kapocsfeszültsége, ha a legtöbb Joule-hőt termelő ellenállás elektromos teljesítménye 360 W?

\(\displaystyle b)\) Mekkora a többi ellenállás teljesítménye?

(4 pont)

A beküldési határidő 2021. május 17-én LEJÁRT.

Megoldás. Számozzuk meg az ellenállásokat az ábrán látható módon. Az 1. ellenálláson folyik át a legnagyobb áram (hiszen az az 1. ellenállás után két részre oszlik), tehát az egyforma ellenállások közül az 1.-re jut a legnagyobb teljesítmény.

Az áramerősség:

\(\displaystyle I=\sqrt{ \frac{P}{R} }=\sqrt{\frac{360~\rm W}{10~\Omega}}=6~\rm A.\)

Ez az áram \(\displaystyle 2:1\) arányban oszlik két részre, a 2. ellenálláson tehát \(\displaystyle 4~\)A, a 3. és 4. ellenálláson pedig 2 A erősségű áram folyik.

\(\displaystyle a)\) Az 1. ellenálláson \(\displaystyle (6~{\rm A})\cdot(10~\Omega))=60~\rm V\) feszültség esik, a 2. ellenálláson pedig 40 V, így a a telep kapocsfeszültsége 100 V.

\(\displaystyle b)\) A 2. ellenállás hőteljesítménye 160 W, a 3. és a 4. ellenállás teljesítménye pedig egyaránt \(\displaystyle 40\) W.

Statisztika:

37 dolgozat érkezett.
4 pontot kapott:	Bacsó Dániel, Beke Botond, Bencz Benedek, Bogdán Benedek, Borsos Balázs, Buzási-Temesi Imre, Cynolter Dorottya, Czirók Tamás, Hegedűs Máté Miklós, Jeney Zsolt, Jeszenői Sára, Kohut Márk Balázs, Kornya Gergely Csaba, Kovács Dorina , Láng Erik, Marozsi Lenke Sára, Molnár Kristóf, Móricz Benjámin, Novák Péter, Országh Júlia, Patricia Janecsko, Richlik Márton, Stein Felix, Szabó Réka, Szanyi Attila, Vágó Botond, Veszprémi Rebeka Barbara, Vincze Farkas Csongor, Waldhauser Miklós.
3 pontot kapott:	Josepovits Gábor.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2021. áprilisi fizika feladatai