 |
A G. 806. feladat (2023. február) |
G. 806. Az ábrán látható kapcsolásban ismert az \(\displaystyle R_1\), \(\displaystyle R_2\) és az \(\displaystyle R_3\) ellenállás, valamint az \(\displaystyle R_3\) ellenálláson átfolyó áram \(\displaystyle I_3\) erőssége.
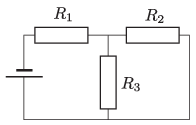
Határozzuk meg
\(\displaystyle a)\) a másik két ellenálláson átfolyó \(\displaystyle I_1\) és \(\displaystyle I_2\) áramok erősségét;
\(\displaystyle b)\) a telep elektromotoros erejét!
\(\displaystyle c)\) Mennyi hő fejlődik összesen \(\displaystyle t\) idő alatt a rendszerben?
(Adatok: \(\displaystyle R_1 = 20~\Omega\), \(\displaystyle R_2 = 10~\Omega\), \(\displaystyle R_3 = 40~\Omega\), \(\displaystyle I_3=2~\mathrm{A}\), \(\displaystyle t=30~\mathrm{s}\).)
(3 pont)
A beküldési határidő 2023. március 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Az \(\displaystyle R_3\) ellenállásra eső feszültség \(\displaystyle U_3=R_3 I_3=80\,\rm{V}\), és ugyanekkora feszültség esik az \(\displaystyle R_2\) ellenállásra is (\(\displaystyle U_2=U_3\)). Ezért az \(\displaystyle R_2\) ellenállás árama \(\displaystyle I_2=U_2/R_2=8\,\rm{A}\). A csomóponti törvény miatt az \(\displaystyle R_1\) ellenálláson átfolyó áram a másik két ellenálláson átfolyó áram összege: \(\displaystyle I_1=I_2+I_3=10\,\rm{A}\).
\(\displaystyle b)\) Az \(\displaystyle R_1\) ellenállásra eső feszültség \(\displaystyle U_1=R_1I_1=200\,\rm{V}\). A huroktörvény alkalmazásával kaphatjuk meg a telep elektromotoros erejét:
\(\displaystyle \varepsilon=U_1+U_2=U_1+U_3=280\,\rm{V}.\)
\(\displaystyle c)\) Az ellenállásokon fejlődő hő megegyezik a telep által leadott energia nagyságával (feltéve, hogy a telep belső ellenállása nulla, vagyis a telep ideális feszültséggenerátor):
\(\displaystyle Q=Pt=\varepsilon I_1t=84\,000\,\rm{J}=84\,\rm{kJ}.\)
Statisztika:
49 dolgozat érkezett. 3 pontot kapott: Antal Áron, Bencze Mátyás, Biró Kata, Bohner Emese, Csapó András, Cseresznye Ákos, Földes Márton, Hornok Máté, Jávor Botond, Ligeti Barnabás, Matyó Simon, Nagy 639 Csenge, Sukola Bence, Sütő Áron, Szatmári Emese, Tajta Sára, Tóth Hanga Katalin, Varga 802 Zsolt, Žigo Boglárka. 2 pontot kapott: Szendrői Bori , Toplak Ágnes, Wolf Erik. 1 pontot kapott: 9 versenyző. Nem versenyszerű: 16 dolgozat.
A KöMaL 2023. februári fizika feladatai
