A G. 819. feladat (2023. május)

G. 819. A képen három, ugyanolyan folyadékot tartalmazó tartály látható, melyekhez leeresztő csövek csatlakoznak. Melyik tartály ürül ki leggyorsabban, ha a folyadék belső súrlódásától (viszkozitásától) eltekinthetünk?

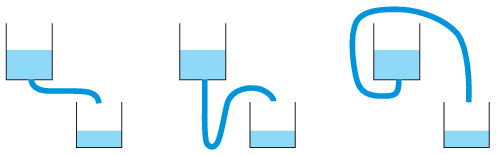
Biztos, hogy a középső tartály egyáltalán kiürül, ha a csatlakozó cső legalja nagyon mélyre kerül? Biztos, hogy a jobb szélső tartály egyáltalán kiürül, ha a csatlakozó cső legteteje nagyon magasra kerül?

(4 pont)

A beküldési határidő 2023. június 15-én LEJÁRT.

Megoldás. A Torricelli-féle kiömlési törvény szerint a kiömlési sebesség csak a cső vége és a folyadék felszíne közötti szintkülönbségtől függ. Ezért mindhárom esetben azonos idő alatt ürül ki a tartály (ha a cső fala okozta fékező hatástól eltekintünk).

A jobb szélső tartály esetében a csatlakozó cső teteje nem kerülhet nagyon magasra (víz esetében ez a határ 10 méter), mert akkor a folyadékban a nyomás már annyira lecsökken, hogy a folyadék cseppekre esik szét. Ugyancsak gondot jelenthet, ha a cső fala viszonylag puha, mert akkor a külső légnyomás teljesen le tudja zárni a csatlakozó csövet (ez közönséges gumicső és víz esetében 1-2 méteres magasság mellett is bekövetkezhet). A középső tartály esetében csak attól kell tartani, hogy igen nagy nyomás elérésekor a csatlakozó cső kidurran.

Statisztika:

25 dolgozat érkezett.
4 pontot kapott:	Antal Áron, Bencze Mátyás, Földes Márton, Nagy 639 Csenge.
3 pontot kapott:	Biró Kata, Varga Zétény.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2023. májusi fizika feladatai