 |
A G. 850. feladat (2024. április) |
G. 850. Mennyi az ábrán látható áramkör eredő ellenállása a telep két kimenete között?
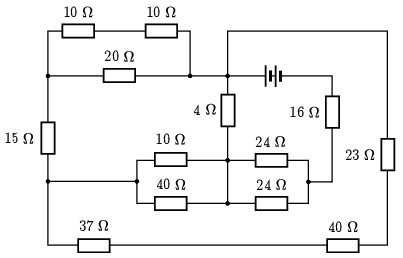
(4 pont)
A beküldési határidő 2024. május 15-én LEJÁRT.
Megoldás. Jelöljük meg a csomópontokat (1. ábra). Azokat a csomópontokat amelyeket (elhanyagolható ellenállású) vezeték köt össze, azonos betűvel jelöljük, hiszen ezek lényegében ugyanazok.
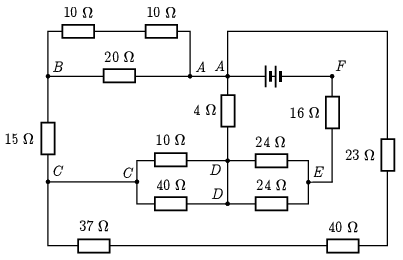
1. ábra
Következő lépésben (2. ábra) összevonjuk az azonos jelű csomópontokat, és a sorosan kötött ellenállásokat: Az \(\displaystyle A\) és \(\displaystyle B\) pont közötti felső ág ellenállása \(\displaystyle R_{AB\textrm{felső}}=10\,\Omega+10\,\Omega=20\,\Omega\), Az \(\displaystyle A\) és \(\displaystyle C\) pontok között a jobb szélen pedig \(\displaystyle R_{AC\textrm{jobb}}=23\,\Omega+40\,\Omega+37\,\Omega=100\,\Omega\).
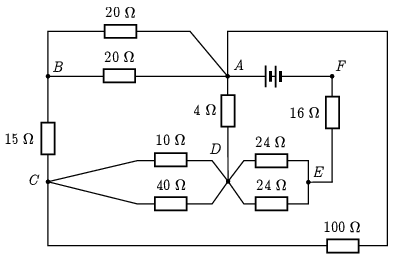
2. ábra
Ezután kiszámítjuk a párhuzamosan kapcsolt ellenállások eredőjét, és ezekkel helyettesítjük a párhuzamosan kapcsolt elemeket. Itt az egyszerűbb írásmód miatt használni fogjuk (a villamosmérnöki gyakorlat alapján) a \(\displaystyle \times\) jelet a ,,replusz'' (reciprokok összegének reciproka) műveletre:
\(\displaystyle R_1\times R_2=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1}.\)
\(\displaystyle R_{AB}=20\,\Omega\times 20\,\Omega=10\,\Omega\), \(\displaystyle R_{CD}=10\,\Omega\times 40\,\Omega=8\,\Omega\), \(\displaystyle R_{DE}=24\,\Omega\times 24\,\Omega=12\,\Omega\). Ezután a \(\displaystyle B\) és \(\displaystyle E\) csomópont meg is szűnik (3. ábra).
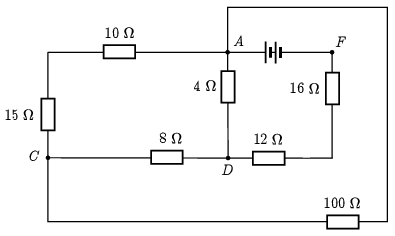
3. ábra
A következő lépés ismét a sorosan kapcsolt ellenállások összevonás. Az \(\displaystyle A\) és \(\displaystyle C\) pontok közötti (bal felső sarokban lévő) két ellenállás eredője \(\displaystyle R_{AC\textrm{balfelső}}=10\,\Omega+15\,\Omega=25\,\Omega\), \(\displaystyle R_{DF}=12\,\Omega+16\,\Omega=28\,\Omega\). Ezzel együtt érdemes az \(\displaystyle A\) és \(\displaystyle C\) pontok közti \(\displaystyle 100\,\Omega\)-os ágat ,,áthajtani'' a bal oldalra (4. ábra).
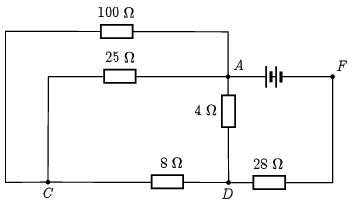
4. ábra
Egyre kevesebb ellenállásunk van, a folyamat felgyorsul: \(\displaystyle R_{AC}=100\,\Omega\times 25\,\Omega=20\,\Omega\) (5. ábra a) rész), így a \(\displaystyle C\) csomópont megszűnik és \(\displaystyle R_{AD\textrm{bal}}=20\,\Omega+8\,\Omega=28\,\Omega\) (5. ábra b) rész), \(\displaystyle R_{AD}=28\,\Omega\times 4\,\Omega=3{,}5\,\Omega\) (5. ábra c) rész), végül \(\displaystyle R_{AF}=3{,}5\,\Omega+28\,\Omega=31{,}5\,\Omega\) (5. ábra d) rész).
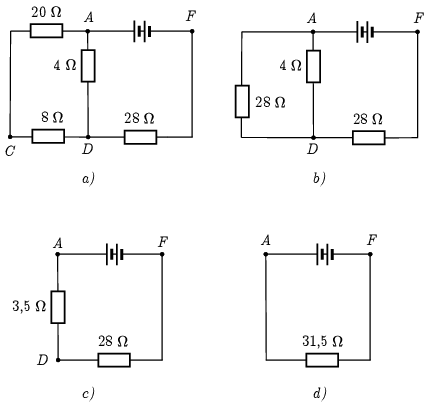
5. ábra
Az eredő ellenállás tehát \(\displaystyle 31{,}5\,\Omega\).
Megjegyzés. Láthatjuk, hogy a végeredményt a \(\displaystyle 4\,\Omega\)-os ellenállás, valamint a \(\displaystyle D\) és \(\displaystyle F\) pontok közötti három ellenállás (ezek eredője az \(\displaystyle R_{DF}=28\,\Omega\)) határozza meg, a többi ellenállásnak (amelyek eredője aztán párhuzamosan van kapcsolva a \(\displaystyle 4\,\Omega\)-ossal) alig van szerepe.
Statisztika:
40 dolgozat érkezett. 4 pontot kapott: Blaskovics Ádám, Bohner Emese, Bús László Teodor, Csáki Anikó, Csonka Áron, Dömők Bernadett, Fülöp Magdaléna, Gerlei Dániel, Görög Csanád Botond, Hrubi kristóf, Jávor Botond, Kámán-Gausz Péter, Kis Boglárka 08, Kisida Kata, Méhes Mátyás , Porcsin Gréta, Sipos Dániel Sándor, Sógor-Jász Soma, Szabó András, Szabó Márton, Táborosi Sára, Tajta Sára, Vértesi Janka, Vincze Anna, Vízhányó Janka, Zhang Yan. 3 pontot kapott: Antal Áron, Barth Albert Krisztián, Havas Dániel. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2024. áprilisi fizika feladatai
