Az I/S. 11. feladat (2016. október)

I/S. 11. Van \(\displaystyle N\) golyónk, ebből \(\displaystyle N-1\) egyforma anyagú, egy golyó pedig különböző. Ránézésre nem tudjuk őket megkülönböztetni, viszont van egy elemző gépünk, ami úgy működik, hogy kiválasztunk \(\displaystyle K\) darab golyót (\(\displaystyle 0< K\le N\)) és a géppel egy elemzés elvégzése után megtudjuk, hogy a különböző golyó a kiválasztott \(\displaystyle K\) darab golyó között van-e. Minden lehetséges \(\displaystyle K\)-ra tudjuk a vizsgálat idejét, vagyis hogy hány percig tart pontosan \(\displaystyle K\) darab golyót megvizsgálni a géppel. Írjunk programot, ami kiszámítja, hogy mi az a legrövidebb időtartam, ami alatt (megfelelő stratégiát követve) meg lehet találni a különböző golyót.

Bemenet: a standard bemenet első sora a golyók \(\displaystyle N\) számát tartalmazza. A második sor \(\displaystyle N\) egész számot tartalmaz, a \(\displaystyle K\)-adik szám (\(\displaystyle L[K]\)) a \(\displaystyle K\) darab golyó megmérésének ideje percben (\(\displaystyle 0< K\le N\)). A mérési idők a golyók darabszáma szerint nemcsökkenő sorozatot alkotnak.

Kimenet: a standard kimenet első és egyetlen sora tartalmazzon egy egész számot, a különböző golyó megtalálásához szükséges legrövidebb időt percben.

Korlátok: \(\displaystyle 1 \le N \le 1000\); \(\displaystyle L[i] \le L[i+1]\) minden \(\displaystyle i\)-re, ahol \(\displaystyle 0< i< N\); \(\displaystyle L[N] \le 10^6\).

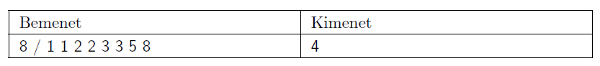
Magyarázat: eredetileg 8 ,,jelöltünk'' van. Megvizsgálunk 4 golyót, ezzel marad 4 jelölt. Ebből megvizsgálunk 2-t, ezután marad 2 jelölt, ezek közül az egyiket megvizsgáljuk. Költség: \(\displaystyle 2+1+1 = 4\).

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes 1 mp alatt megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített is11.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2016. november 10-én LEJÁRT.

Mivel a mérési költségek nemcsökkenő sorozatot alkotnak, nincs értelme olyan golyót a mérlegre tenni, amiről tudjuk, hogy nem a speciális golyó. Viszont minden mérés után, ha \(\displaystyle K\) golyót mérünk meg, akkor vagy erről a \(\displaystyle K\) golyóról, vagy a maradék \(\displaystyle N-K\) golyóról biztosan tudni fogjuk, hogy nincs köztük a speciális golyó.

Vagyis a helyzet mindig leírható egy pozitív egész számmal: azon golyók számával, amelyekről még nem tudjuk, hogy speciálisak-e.

Ha egy golyónk van, akkor az biztosan a speciális golyó, vagyis végeztünk,

különben pedig ha \(\displaystyle G\) golyónk van, akkor megmérhetünk \(\displaystyle 1\), \(\displaystyle 2\), ... vagy \(\displaystyle G-1\) golyót. Ha \(\displaystyle K\) golyót mérünk meg, akkor a mérés eredményétől függően vagy \(\displaystyle K\), vagy \(\displaystyle G-K\) golyó marad. Vegyük észre, hogy amennyiben minden \(\displaystyle G\)-nél kisebb helyzetre ismerjük az optimális megoldást, akkor minden \(\displaystyle K\)-ra meg tudjuk mondani, hogy ha \(\displaystyle K\) golyót mérünk meg, akkor legrosszabb esetben mennyi ideig tart a keresés. Innen következik, hogy ha minden lehetséges \(\displaystyle K\)-ra kiszámítjuk ezt, és vesszük a legkisebb értéket, akkor megtaláljuk az optimális megoldást \(\displaystyle G\) golyóra.

Láthatjuk, hogy ez egy dinamikus programozási feladat, a futási idő \(\displaystyle O(N^2)\), a memóriahasználat \(\displaystyle O(N)\).

Megjegyzés: Észrevehetjük, hogy ha \(\displaystyle K\) golyót mérünk meg, azzal ugyanazt az eredményt érjük el, mintha a másik \(\displaystyle G-K\) golyót mértük volna meg, ezért mivel a mérési költségek nemcsökkenő sorozatot alkotnak, elég ha a minimum értéket csak \(\displaystyle K=1, \ldots , \lfloor \frac {G} {2} \rfloor\)-re nézzük meg, mivel a minimum biztosan ezek között lesz, de ez nem javít a futási idő komplexitásán, és a maximális pontszám megszerzéséhez nem szükséges.

main.cpp

Statisztika:

20 dolgozat érkezett.
10 pontot kapott:	Bálint Martin, Borbényi Márton, Csenger Géza, Földes András Ottó, Gáspár Attila, Gergely Patrik, Horváth Botond István, Janzer Orsolya Lili, Kiss Gergely, Kovács 246 Benedek, Molnár Bálint, Nagy Nándor, Szakály Marcell, Vári-Kakas Andor.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. októberi informatika feladatai