 |
Az I/S. 57. feladat (2021. november) |
I/S. 57. Adott egy \(\displaystyle N\) elemű \(\displaystyle T\) tömb, amelynek az \(\displaystyle i\)-edik elemét \(\displaystyle T[i]\)-vel jelöljük \(\displaystyle (1 \le i \le N)\). A tömb összes eleme pozitív, \(\displaystyle N\)-nél nem nagyobb egész szám. A tömb leggyakoribb elemei közé akkor tartozik egy \(\displaystyle x\) szám \(\displaystyle (1 \le x \le N)\), ha nincs olyan másik \(\displaystyle y\) szám \(\displaystyle (1 \le y \le N)\), ami többször fordul elő \(\displaystyle T\)-ben, mint \(\displaystyle x\).
Módosításnak nevezzük azt, ha az eredeti \(\displaystyle T\) tömb egy elemét megváltoztatjuk egy tetszőleges pozitív, \(\displaystyle N\)-nél nem nagyobb egész számra. Két módosítás különböző, ha különböző elemét módosítjuk \(\displaystyle T\)-nek, vagy ugyanazt az elemét módosítjuk, de más értékre.
Adjuk meg minden \(\displaystyle x\) számra \(\displaystyle (1 \le x \le N)\), hogy hány olyan módosítás van, aminek a végrehajtása után a kapott tömbnek \(\displaystyle x\) egy leggyakoribb eleme lesz.
Bemenet: az első sorban az \(\displaystyle N\) szám található. A következő sorban \(\displaystyle N\) darab szám található: a \(\displaystyle T\) tömb elemei.
A kimenet egyetlen sorában adjunk meg \(\displaystyle N\) darab számot: az \(\displaystyle i\)-edik szám azon módosítások száma legyen, amikor \(\displaystyle i\) egy leggyakoribb elem.
Példa:
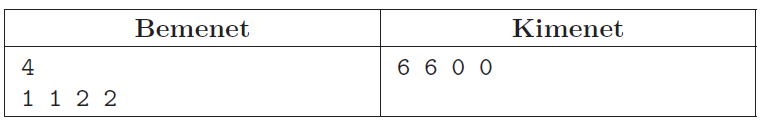
Magyarázat: az 1 egy leggyakoribb elem lesz, a 3. vagy 4. elemet bármilyen lehetséges értékre módosítjuk. Ez összesen \(\displaystyle 3 + 3 = 6\) eset. Ehhez hasonlóan lehet a 2 egy leggyakoribb elem. A 3 vagy a 4 nem lehet egy leggyakoribb elem.
Korlátok: \(\displaystyle 1 \le N \le 1000\), \(\displaystyle 1 \le T[i] \le 1000\). Időlimit: 0,3 mp.
Értékelés: a pontok 50%-a kapható, ha a program az \(\displaystyle 1 \le N \le 10\) elemszámú tesztesetekre helyes megoldást ad.
Beküldendő egy is57.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
A beküldési határidő 2021. december 15-én LEJÁRT.
Statisztika:
8 dolgozat érkezett. 10 pontot kapott: Kovács Alex, Tóth 057 Bálint. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2021. novemberi informatika feladatai
