Az I. 153. feladat (2007. február)

I. 153. Készítsünk táblázatkezelő alkalmazást, amely egy függőlegesen fölfelé kilőtt golyó mozgását szemlélteti. A megoldást tartalmazó munkafüzetben az ,,Adatok'' munkalap tartalmazza a mozgással kapcsolatos adatokat, a ,,Grafikon'' munkalap mutassa be a mozgás hely-idő, sebesség-idő és gyorsulás-idő függvényét, a ,,Számítások'' munkalap tartalmazza a szükséges számításokat.

Az adatokat tartalmazó munkalap A1:B7 tartományában - az alábbi mintához hasonlóan - szerepeljenek a golyó és a kilövés adatai, a számításokhoz szükséges állandók:

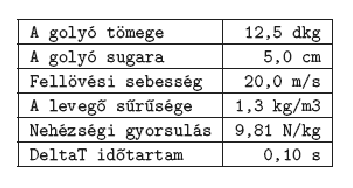
A kilőtt golyó helyének, sebességének és gyorsulásának kiszámítása szimulációs lépésekben a kezdeti értékek, illetve az előzőleg számított eredmények alapján történjen. A számításokat tartalmazó munkalap 200 szimulációs lépéssel dolgozzon, a lépések között a fent megadott időtartam teljen el. A grafikon e számítások eredményeit mutassa be, azonos időtengelyen ábrázolva a mozgást leíró függvényeket.

Beküldendő a megoldást tartalmazó táblázatkezelő munkafüzet (i153.xls, i153.xsc, ).

(10 pont)

A beküldési határidő 2007. március 19-én LEJÁRT.

A feladat megoldásánál felhasználtuk, hogy egy a közeghez képest v sebességgel mozgó testre a mozgás irányával szemben F_k=-kA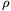v² nagyságú közegellenállási erő hat. A feladat kitűzésében a k alaki tényező nem szerepelt, ennek hiányáért nem vontunk le pontot (gömb esetén k=0,45).

Az aktuális ható erő és a nehézségi erő összegéből Netwon II. törvénye alapján megkapható a test pillanatnyi gyorsulásának értéke. Ebből a pillanatnyi sebesség, és a test elmozdulása az eltelt t idő figyelembe vételével: y=vt, valamint v=at.

A megoldás részletei a mellékelt (i153.xls) Excel táblázatban találhatók.

Statisztika:

17 dolgozat érkezett.
10 pontot kapott:	Berzlánovich Imre, Czigler András, Fábián András, Földes Imre, Gombos Gergely, Györök Péter, Kovács 129 Péter, Ridinger Tamás, Szoldatics András, Vincze János.
9 pontot kapott:	Danka Miklós András, Véges Márton.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	2 versenyző.

A KöMaL 2007. februári informatika feladatai