 |
Az I. 188. feladat (2008. május) |
I. 188. Aristid Lindenmayer (1925-1989), magyar származású holland biológus, matematikus a növényi fejlődést tanulmányozta algoritmusokkal. Szöveges képletekkel (generatív nyelvtannal) leírható vonalas fraktálokkal foglalkozott. Rendszerét nevének kezdőbetűje alapján L-Systemnek nevezik és ezt a teknőcgrafika előfutárának tekinthetjük. Szimbólumai a toll mozgásirányának és lépései hosszának információit hordozzák.
A fraktál rajzolásához egy axióma, egy szabály és a fordulás szöge szükséges. Az ábrák finomságát, felbontását a rekurzív helyettesítések száma adja meg.
Az egyik legismertebb vonalas fraktál a Koch-görbe.
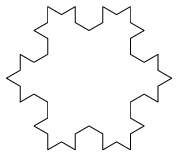
Axióma: F
Szabály: F=F+F-F+F
Szög: 60
Helyettesítés: 3
Mi történik, ha az axiómát bővítjük?
A szabály a rekurzív helyettesítés formuláját adja.
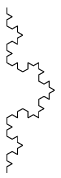
Axióma: F-F-F
Szabály: F=F+F-F+F
Szög: 60
Helyettesítés: 3
Készítsük el az öt ábrán látható L-System fraktált az ingyenesen letölthető Inkscape vektorgrafikus rajzoló programmal. A 6. ábra saját alkotás legyen.
A programban kissé eldugott helyen található az L-System ábrákat generáló funkció. Indítás helye: Effektusok / Megjelenítés / L-rendszer.
Axióma és szabály elemek az Inkscape L-rendszerben:
|
Példa a verem használatára egy fa rajzolásánál:
|
Az elkészített ábrák könnyen színezhetők a vektorgrafikus rajzoló programmal.
Beküldendő az ábrákat leíró paraméterek listája (axióma, szabály, szög és a helyettesítések száma) egy rövid dokumentációban (i188.txt, i188.doc, ), valamint egy szabadon alkotott 6. ábra és annak paraméterlistája (i188.svg, i188.png, ...).
Az elkészítendő ábrák:
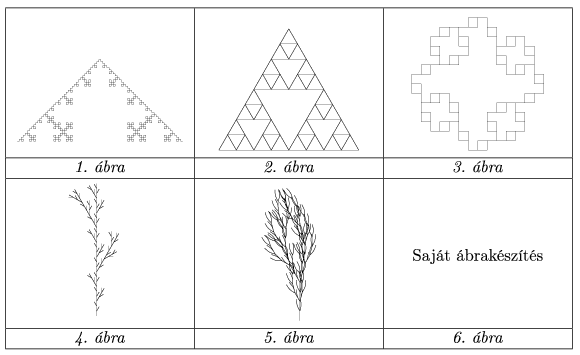
(10 pont)
A beküldési határidő 2008. június 16-án LEJÁRT.
Megoldás
A feladatra sok jó megoldás érkezett. Néhány ábra előállítható többféle axiómával és szabállyal is. Lindenmayer munkásságáról sok cikket olvashatunk. Most egyet ajánlok figyelmetekbe.
|
A szabadon választott 6. ábrának nagyon szép és látványos rajzok érkeztek. Többen a kész ábra színezésével is foglakoztak.
Példaként álljon itt Horváth 135 Lóránd rajza:

Statisztika:
7 dolgozat érkezett. 10 pontot kapott: Fábián András, Földes Imre, Horváth 135 Loránd, Pap 987 Dávid, Póta Kristóf, Véges Márton. 6 pontot kapott: 1 versenyző.
A KöMaL 2008. májusi informatika feladatai
