Az I. 259. feladat (2011. február)

I. 259. A rekurzió a matematikában és az informatikában gyakran használt eszköz. A probléma megoldás különböző fázisaiban, így a specifikációban, az algoritmikus tervezésben és a programnyelven történő kódolásban fordulhat elő.

A specifikáció megadására függvényt szokás használni, amely a bemenet és a kimenet között hatékonyan adja meg a kapcsolatot. Kezdésként nézzük a hatványozás műveletét. Ennek definíciója: \(\displaystyle x^{n} =x\cdot x^{n-1}\), és \(\displaystyle x^{0}=1\), másképpen:

\(\displaystyle \mathop{\text{hatvány}}\, (x,n)= \begin{cases} 1 & \text{ha } n=0, \\ x\cdot \mathop{\text{hatvány}}\, (x,n-1) & \text{ha } n>0. \end{cases} \)

Így tehát az \(\displaystyle 5^{3}\)-t visszavezetjük \(\displaystyle 5\cdot 5^{2}\)-ra, vagyis \(\displaystyle 5^{2}\)-ra, azt \(\displaystyle 5^{1}\)-re, végül azt az \(\displaystyle 5^{0}\)-ra, amit már nem vezetünk vissza. A feladat rekurzív algoritmussal hatékonyan megoldható:

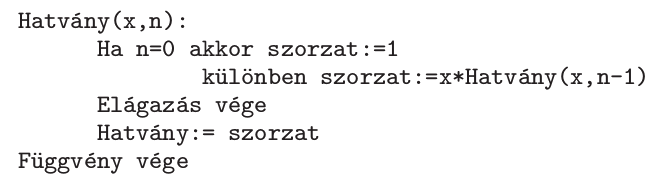
Funkcionális programozási nyelven, például Imagine Logo-ban a kódolás természetesen következik:

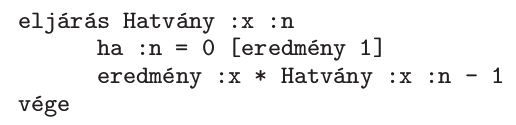
A nemrekurzív nyelvek is engedélyezhetik a kódolást, így például Pascal nyelven a kód:

Az iteratív módon meghatározott algoritmusok, programok átírhatók rekurzívvá. A legfontosabb algoritmikus egységekkel, a szekvenciával és az elágazással nincs gond, változtatás nélkül átvihetők. A ciklust tartalmazó eljárásokat kell rekurzívvá tenni. Az elöltesztelő ciklus átírása:

Minta: Állítsuk elő a természetes számok sorozatát \(\displaystyle A\)-tól \(\displaystyle B\)-ig (\(\displaystyle 1\le A,B\le 100\)). Például az Előállít(5, 10, Sor, 1) eljárás a Sor tömbbe elhelyezi az 5 6 7 8 9 10 számsort.

I. Iteratív megoldás:

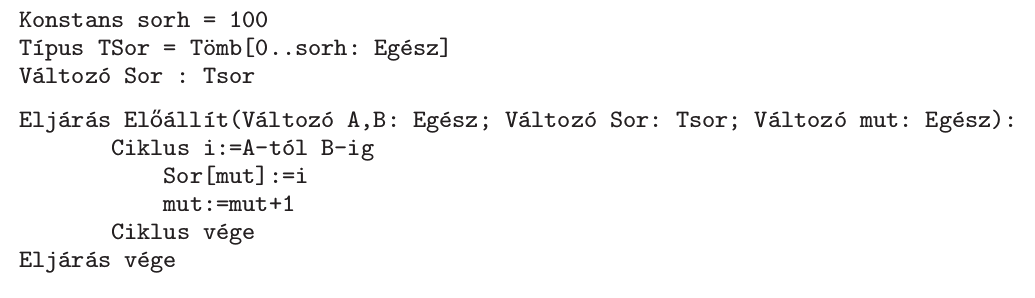
II. Rekurzív megoldás:

Készítsünk programot, amely számsorozatokat állít elő úgy, hogy a programban ciklus utasítást nem használunk.

\(\displaystyle a)\) Írjunk függvényt, ami egy \(\displaystyle N\) (\(\displaystyle N\ge 1\)) magas számhegyet hoz létre! Példa: számhegy 5 Eredménye: 1 2 3 4 5 4 3 2 1;

\(\displaystyle b)\) Írjunk függvényt, ami egy \(\displaystyle N\) magas számhegységet hoz létre! Példa: számhegység 4 Eredménye: 1 1 2 1 1 2 3 2 1 1 2 3 4 3 2 1;

\(\displaystyle c)\) Írjunk függvényt, ami egy \(\displaystyle N\) magas számlépcsőt hoz létre! Példa: számlépcső 6 Eredménye: 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6;

\(\displaystyle d)\) Írjuk fel az alábbi, rekurzív képlettel megadott sorozat első \(\displaystyle N\) elemét: \(\displaystyle a_{1}=-1\) és \(\displaystyle a_{n}=-4 - 3a_{n-1}\).

A program első argumentuma \(\displaystyle N\) értéke és a második egy kimeneti fájl legyen. A kimeneti fájlban soronként jelenítsük meg a sorozatok szóközzel elválasztott elemeit. (A fájlba íráskor se használjunk ciklust.)

Beküldendő a program forráskódja (i259.pas, i259.cpp, ...), valamint a program rövid dokumentációja (i259.txt, i259.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2011. március 10-én LEJÁRT.

Mintamegoldásként Szabó Attila (Pécs, Leőwey Klára Gimnázium, 10. osztály) tanuló munkáját közöljük: i259.pas

Statisztika:

11 dolgozat érkezett.
10 pontot kapott:	Gema Barnabás, Hoffmann Áron, Kalló Kristóf, Seres Márk Dániel, Szabó 928 Attila.
9 pontot kapott:	Barta 111 János, Kocsis 789 Mátyás, Leitereg András, Sztanka-Tóth Tamás, Varga 256 Erik.
7 pontot kapott:	1 versenyző.

A KöMaL 2011. februári informatika feladatai