 |
Az I. 280. feladat (2011. december) |
I. 280. Szilárd anyagokon folyadék átszivárgásának vizsgálatára, perkolációjára az I. 271. feladat statisztikai modell program készítését kérte. Egy n×n-es (1
n50) négyzet alakú terület -- az anyag függőleges metszete -- minden cellája p (0,00p1,00) valószínűséggel átengedi a folyadékot (például egy mikrorepedés alakul ki), és 1-p valószínűséggel pedig nem. Modellünket azzal bővítjük, hogy feltételezzük, a folyadék nyomása biztosítja, hogy a repedéshálózatban tetszőleges irányba, akár felfelé is áramolhat a folyadék. Az ábrán látható anyag átengedi a folyadékokat.
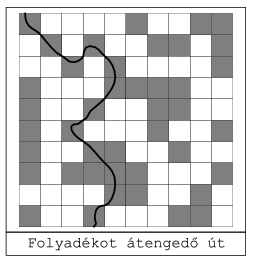
A lehetséges lépésirányok a cellák között a 8 szomszéd felé mutatnak. Készítsünk programot, amely a p valószínűség 0-ról való növelésével megkeresi az első átengedő állapotot. A négyzet n oldalhossza a megadott feltételek között tetszőleges lehet. A p valószínűség értékét 0,05-dal növeljük, amíg átengedő állapotot nem generálunk. Elegendő minden p értéknél egy táblázatot készíteni. Ezt az állapotot tetszőleges módon jelenítsük meg a képernyőn, amelyen az át- és nem átengedő cellákat, valamint egy lehetséges átvezető utat lehessen látni.
Beküldendő egy tömörített i280.zip állományban a program forráskódja (i280.pas, i280.cpp, ...), és a program rövid dokumentációja (i280.txt, i280.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2012. január 10-én LEJÁRT.
Mintamegoldásként Barkaszi Richárd Miklós 12. osztályos (Nyíregyháza, Széchenyi István Közgazdasági Szakközépiskola) tanuló munkáját közöljük: i280.pas
Kucsma Levente István 9. osztályos (Eger, Dobó István Gimnázium) megoldásának egy érdekes eredménye:
Statisztika:
14 dolgozat érkezett. 10 pontot kapott: Adrián Patrik, Antal János Benjamin, Barkaszi Richárd Miklós, Beleznay Soma, Fényes Balázs, Hoffmann Áron, Kovács Balázs Marcell, Kucsma Levente István, Szabó Levente, Varga 256 Erik, Veress Péter. 9 pontot kapott: Jákli Aida Karolina, Kocsis 789 Mátyás. 8 pontot kapott: 1 versenyző.
A KöMaL 2011. decemberi informatika feladatai