Az I. 307. feladat (2012. december)

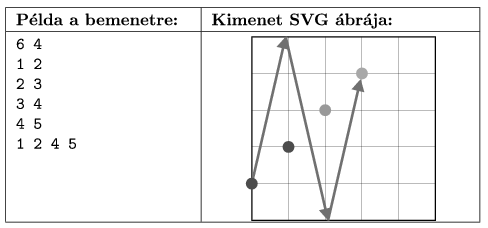
I. 307. Biliárdgolyók útvonalát vizsgáltuk az I. 298. feladatban. Adott egy négyzet alakú biliárdasztal, amelynek szélén a golyók tökéletesen rugalmasan ütközhetnek. A golyók kiterjedés nélküliek, egymással szintén tökéletesen rugalmasan ütközhetnek és az asztal egész koordinátájú pontjaiban állhatnak.

Készítsünk programot i307 néven, amely elkészíti a paraméterek beolvasása után egy kétpattanásos golyóútvonal ábráját egy SVG típusú vektorgrafikus képállományba. A golyó egy adott (k;l) koordinátájú pontból gurítva az adott (x;y) koordinátájú golyót találja el.

A golyó két falon pattanjon vissza és más golyóval történő ütközéstől eltekintünk. Ennek oka, hogy a tökéletesen rugalmas, centrálisan történő ütközésnek megfelelően az eltalált golyó az őt eltaláló golyó mozgásának irányában folytatja a mozgását. Ha egy golyó pont az asztal sarkát találja el, akkor önmagába verődik vissza és ez két visszapattanásnak számít. A program eredménye a biliárdasztal, a golyók és a kétpattanásos pálya ábrázolása szakaszokkal (nyilakkal) SVG állományban.

SVG ábra generálása szerepelt az I. 243. feladatban, illetve az ábra szerkezetéről olvashatunk a http://svg.elte.hu/ címen.

A grafikai elemek tulajdonságait (színüket, vonalvastagságukat stb.) tetszőlegesen állíthatjuk be.

A program parancssori argumentuma legyen a kezdő feltételeket leíró adatállomány neve. A fájl első sorában N (2N50) az asztal méretét, M (1<M20) a golyók számát adja meg. Az ezt követő M sor a golyók koordinátáit, majd az utolsó sor a golyóindítás (k;l) koordinátáit (1k;lN), és a célgolyó (x;y) koordinátáit írja le. A biliárdasztal bal alsó sarka az (1;1) koordinátájú pont, és az 1. koordináta jobbra, a második koordináta felfelé nő.

Beküldendő egy tömörített i307.zip állományban a program forráskódja (i307.pas, i307.cpp, ...) és rövid dokumentációja (i307.txt, i307.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2013. január 10-én LEJÁRT.

Mintamegoldás:

Fényes Balázs 10. évfolyamos tanuló (Budapest, Szerb Antal Gimnázium) i307.cs és leírása. Néhány ábra a versenyzők munkájából a következő tesztadatokra:

Fényes Balázs ábrája

Gema Barnabás 12. évfolyamos tanuló (Veszprém, Lovassy László Gimnázium) ábrája:

Jákli Aida Karolina 10. évfolyamos tanuló (Zalaegerszeg, Zrínyi Miklós Gimnázium) ábrája:

Qian Lívia 10. évfolyamos tanuló (Szeged, SZTE Ságvári E. Gyakorló Gimnázium) ábrája:

Varga Erik 12. évfolyamos tanuló (Budapest, Berzsenyi Dániel Gimnázium) ábrája:

Hornák Bence 9. évfolyamos tanuló (Budapest, Berzsenyi Dániel Gimnázium) ábrája:

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Fényes Balázs, Gema Barnabás, Hornák Bence, Jákli Aida Karolina, Qian Lívia, Varga 256 Erik.
5 pontot kapott:	1 versenyző.

A KöMaL 2012. decemberi informatika feladatai