Az I. 308. feladat (2012. december)

I. 308. A Forma-1-es verseny 1986-ban jutott el hazánkba. Ennek a versenyévnek adatait dolgozzuk fel az alábbi feladatban.

A megoldáshoz az 1986.txt UTF-8 kódolású, tabulátorral tagolt, honlapunkról letölthető szövegfájlt használjuk.

Ahol csak lehetséges, alkalmazzunk - lehetőség szerint másolható - képletet.

[1.] Az 1986.txt fájl tartalmát helyezzük el a  Helyezések munkalapon az A1 cellától kezdődően.

[2.] A Helyezések munkalap 1. sorának adatait másoljuk át a Pontszámok munkalap B6-os cellájától kezdődően, az A és B oszlopok tartalmát pedig az átmásolt sorhoz illeszkedően.

A további feladatok a Pontszámok munkalapra vonatkoznak.

[3.] A D7:S36 tartományban határozzuk meg a pilóták egyes futamokon szerzett pontszámát. Az 1., 2., ..., 6. helyezés sorrendben 9, 6, 4, 3, 2, 1 pontot ér. Ügyeljünk arra, hogy azon futamok cellája üresen maradjon, ahol a versenyző nem szerzett pontot. A pontszám meghatározásához alkalmas segédtábla készíthető a Helyezések munkalap A40-es cellájától kezdődően.

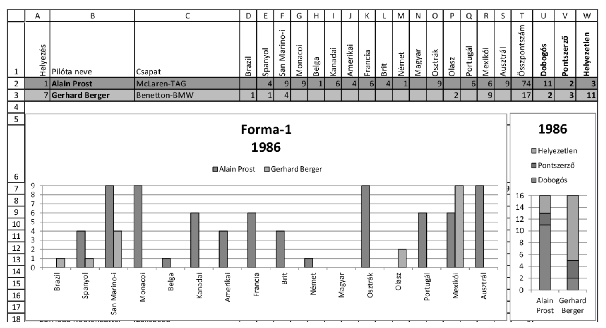
[4.] A T6 cellába jegyezzük be az Összpontszám szöveget, majd alatta határozzuk meg az egyes versenyzők által az 1986-os évben szerzett összes pontot.

[5.] Az A6-os cellába írjuk be a Helyezés szöveget, majd alatta az összpontszám alapján határozzuk meg a versenyzők helyezését.

[6.] Az első sor tartalmát alakítsuk ki a mintának megfelelően. A B2, B3 cellákba egy-egy versenyző nevét bejegyezve határozzuk meg az A2:A3 és C2:T3 cellák értékét a teljes tartományon belül hibamentesen másolható képlet segítségével.

[7.] Az U1:W1 cellákat töltsük ki a minta alapján, majd az U2:W3 cellákat értelemszerűen adjuk meg a megfelelő képlettel.

[8.] Ábrázoljuk oszlopdiagramon a két választott versenyző egyes versenyeken szerzett pontjait. Egy másik diagram pedig mutassa meg a két versenyző dobogós, pontszerző és helyezetlen versenyeredményeinek arányát. A diagramokat az 5. sortól, a felette kitöltött oszlopok szélességében helyezzük el.

[9.] A táblázatban a 2-3. sort színezzük a diagram oszlopszíneivel egyezően. Az A1:W3 tartományt formázzuk a minta alapján.

Beküldendő a megoldást adó munkafüzet (i308.xlsx, i308.ods, ...), a használt program verziószámát és a megoldás lényegét tartalmazó leírás (i308.txt, i308.pdf, ...) egy fájlba tömörítve (i308.zip).

Forrás: 1986.txt

(10 pont)

A beküldési határidő 2013. január 10-én LEJÁRT.

Az érettségi típusú feladatban az alábbi részfeladatok számítottak nehezebbnek:

F3. Legtöbben az Fkeres függvényt használták, de meglepően sokan választották az egymásba ágyazott Ha függvényt is.

F5. A helyezés megállapítására a Sorszám függvény a legalkalmasabb, de megfelelő paraméterezéssel a Darabteli függvény is helyes eredményt ad.

F6. A teljes megadott tartományban (még az A2, A3 cellákban is!) működik az Index-Hol.van páros, de az - első oszlop celláit kivéve - az Fkeres függvény is teljesíti a feladat követelményeit, ha az oszlop számánál az Oszlop függvényt is használjuk.

F7. A feladatot általában a Darab függvények megfelelő elemével oldották meg a beküldők.

F8. A diagram készítésénél többen vesztettek pontot a skála megfelelő beállításánal elmulasztásával.

Sokan hibátlan megoldást adtak a feladatra - ahogy ez el is várható egy érettségi feladat esetében. A feladathoz mellékelt, a megoldás menetét mutató leírás terjedelmét és minőségét tekintve elég vegyesnek bizonyult. Az értékelésben a dokumentációért 10 százalékot ért.

A több jó közül a legegyszerűbb megoldás Gema Barnabásé volt: i308.xlsx

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Gema Barnabás, Jákli Aida Karolina, Láposi Viktória, Qian Lívia, Tegzes Tamás.
9 pontot kapott:	Farkas 1230 Gábor, Fényes Balázs, Szőts Dávid István, Tomku György.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	1 versenyző.

A KöMaL 2012. decemberi informatika feladatai