Az I. 406. feladat (2016. szeptember)

I. 406. Különböző élhosszúságú kockákból tornyokat építünk, és azokat kívülről lefestjük egy automatával. A tornyoknak stabil felépítésűeknek kell lenniük, majd festésükkor az automata mind a négy oldalról és felülről lefesti azokat.

Rendelkezésre áll \(\displaystyle K\) darab kocka véletlenszerű sorrendben. A kockák élhosszai egész számok. Az automata programja szerint igyekszik minél magasabb tornyot építeni, majd befesteni a következő szabályok szerint:

– A kockákat sorrendben egymás után használja föl.

– Kockát olyan torony tetejére tehet, ahol az eddigi legfelső kocka nem kisebb az elhelyezendőnél.

– A soron következő kockát arra a toronyra teszi, ahol a legfelső a lehető legkisebb olyan, amire még rátehető. Ha több ilyen torony van, akkor a kisebb sorszámút (amelyiket előbb kezdte el építeni) választja. Amennyiben a kocka egyikre sem tehető, akkor új tornyot kezd.

– Miután a kockák elfogytak, a kész tornyokat festékszóró festi be minden oldalról és felülről, de alulról és a kockák között nem.

Rendelkezésünkre áll és a honlapunkról letölthető egy minta az automata bemenetére a kockak.txt állományban.

Az állomány első sorában \(\displaystyle K\) (\(\displaystyle 0\le K\le 1\,000\)) a kockák száma olvasható, az ezt követő \(\displaystyle K\) sor mindegyike az egyes kockák \(\displaystyle M_i\) élhosszát (\(\displaystyle 1\le M_i \le 50\)) tartalmazza.

Készítsünk programot i406 néven, amely megoldja az alábbi feladatokat.

A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk a képernyőre a feladat sorszámát (például 4. feladat:). A beolvasás előtt a várt tartalomra vonatkozó üzenetet jelenítsünk meg. Az ékezet nélküli kiírás is megengedett.

1. Olvassuk be a kockak.txt állomány adatait és a következő feladatokat ezek alapján oldjuk meg.

2. Írjuk ki a képernyőre az automata által felépített tornyok számát.

3. Írjuk a képernyőre egy sorba, szóközzel elválasztva a legmagasabb tornyot alkotó kockák élhosszúságát és ezek összegét, vagyis a torony magasságát. Ha több ilyen van, akkor a legkisebb sorszámú toronyét jelenítsük meg.

4. Írjuk a képernyőre annak a toronynak a sorszámát, amelyben a legtöbb azonos élhosszúságú kocka van (több ilyen torony esetén a legkisebb sorszámút).

5. Szabályosnak nevezünk egy legalább 3 kockából álló tornyot akkor, ha a kockák oldalélei alulról felfelé haladva számtani sorozatot alkotnak. Írjuk a képernyőre a szabályos tornyok számát.

6. Kérjük be a felhasználótól egy torony sorszámát, majd írjuk ki szóközzel elválasztva egy sorba, hogy

\(\displaystyle a.\) mekkora területet festett be az automata a tornyon;

\(\displaystyle b.\) a tornyot szétszedve a kockákon összesen hány területegységet nem festett be az alsó oldalakat is figyelembe véve.

7. Írjuk a képernyőre, hogy az első torony felső szintjeiből hány kockát lehetne a legutolsó toronyra átrakni egyben, a méretre vonatkozó szabályok betartásával.

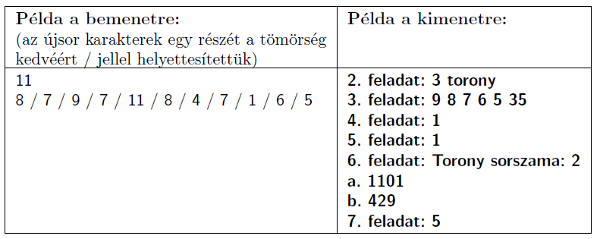
Beküldendő egy tömörített i406.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

Letölthető fájl: kockak.txt.

(10 pont)

A beküldési határidő 2016. október 10-én LEJÁRT.

Mintamegoldás:

Kis Lázár Bence 11. osztályos tanuló Dunaszerdahely, Magyar Tanítási Nyelvű Magángimnázium megoldása: i406.cpp

Statisztika:

15 dolgozat érkezett.
10 pontot kapott:	Földi Dániel, Horváth 237 Lili, Józsa Richárd, Kis Lázár Bence, Merkl Gergely, Rittgasszer Ákos, Szakali Benedek, Szinyéri Bence.
9 pontot kapott:	Békési Péter, Papatyi Dániel.
8 pontot kapott:	2 versenyző.
6 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. szeptemberi informatika feladatai