 |
Az I. 409. feladat (2016. október) |
I. 409. A Tóték Zrt. különböző méretű, téglatest alakú dobozok készítésével foglalkozik. A dobozok mindegyik oldaléle centiméterben mérve pozitív egész szám. A dobozokat nem lehet szétszedni, de könnyen egymásba pakolhatók, ha a kisebbik doboz megfelelő oldalélei kisebbek a nagyobbik doboz megfelelő oldaléleinél.
Egy futószalagon egymás után helyezkednek el a műhely gyártósoráról érkező dobozok. A cég alkalmazottja az elárusító helyre történő szállítás előtt igyekszik úgy egymásba helyezni a dobozokat, hogy azok minél kevesebb helyet foglaljanak el. Módszere a következő: elindul a futószalag elejétől, és megnézi, hogy a második doboz egymásba helyezhető-e az elsővel. Ha igen, akkor a nagyobbikba beleteszi a kisebbiket, és ezután az így keletkező kétdobozos doboz lesz az első kettő helyén, és most a kezdetben harmadik helyen álló dobozt veti össze az előbb keletkezett dupla dobozzal. Ha ezek is egymásba helyezhetők – akár úgy, hogy az új doboz lesz középen – akkor elvégzi a dobozolást. Ha az első két doboz nem helyezhető egymásba, akkor szintén a harmadik dobozt veti össze az előtte lévővel, ami most a második, és egymásba helyezi őket, ha lehet. Ugyanígy jár el a következő dobozzal, majd a rá következővel, és így tovább az összessel. Vagyis minden esetben egy dobozt próbál összevonni a közvetlenül előtte lévő másik dobozzal vagy dobozcsoporttal.
Segítsünk az alkalmazottnak elvégezni a dobozolást! Készítsünk programot, amely a szalagon lévő dobozok méretei alapján megadja, hogy milyen egymásba helyezés alakítható ki a fenti módszerrel. A standard bemenet első sorában a szalagon érkező dobozok száma található. A bemenet minden további sorában három pozitív egész adja meg az egymás után jövő dobozok három oldalélének nagyságát centiméterben. A standard kimenetre írjuk a dobozolás után kialakított helyzetet: az első sorba a futószalagon most látható dobozok darabszámát, majd az utána következő sorok mindegyikébe írjuk az egyedül álló vagy egymásba ágyazott dobozok eredeti elhelyezkedés szerinti sorszámát. Amennyiben a külső dobozban vannak dobozok, akkor azok sorszáma méret szerint csökkenő sorrendben legyen fölsorolva az adott sorban.
Példaként nézzük meg a következő be- és kimenetet, ahol a tömörség kedvéért a sorvége jelek egy részét / jellel helyettesítettük:
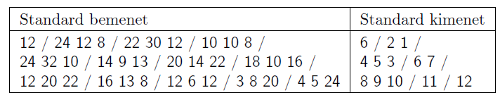
A futószalagon legalább 2, de legföljebb 200 doboz található, melyek mindegyikének mindhárom oldaléle centiméterben mérve 1 és 100 közötti pozitív egész.
Beküldendő egy tömörített i409.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2016. november 10-én LEJÁRT.
Mintamegoldásként Békési Péter, 9. évfolyamos zalaegerszegi versenyző (i409bpdoku.pdf, i409bp.vb), és Kis Lázár Bence 11. évfolyamos dunaszerdahelyi (i409klbdoku.pdf, i409klb.cpp) versenyző munkáit adjuk közre.
Statisztika:
10 dolgozat érkezett. 10 pontot kapott: Békési Péter, Horváth 237 Lili, Kis Lázár Bence, Kovács 246 Benedek, Papatyi Dániel, Rittgasszer Ákos, Szakali Benedek, Tersztenyák Balázs. 8 pontot kapott: 1 versenyző. 7 pontot kapott: 1 versenyző.
A KöMaL 2016. októberi informatika feladatai
