Az I. 413. feladat (2016. november)

I. 413. Ábrázoljunk közös koordináta-rendszerben egy origó középpontú kört és egy azt metsző egyenest, valamint határozzuk meg a metszéspontjaik koordinátáit három tizedesjegy pontossággal táblázatkezelő segítségével.

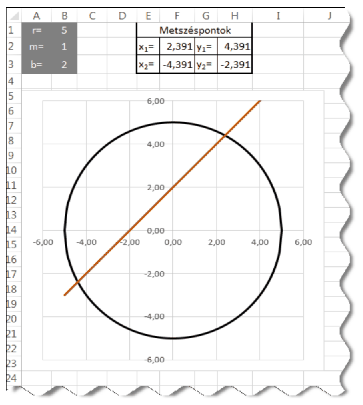
A kör az \(\displaystyle x^{2} + y^{2} = r^{2}\) és az egyenes az \(\displaystyle y = mx + b\) egyenlettel van megadva. Alakítsuk ki a minta szerinti táblázatszerkezetet és a feliratokat készítsük el. A J oszloptól jobbra segédszámításokat végezhetünk, amelyek értelmezését feliratokkal segítsük elő. Állítsuk be, hogy a felhasználó csak a B1:B3 tartomány értékeit módosíthassa, de bármely cella tartalmát megtekinthesse. A hibás adatbevitelt akadályozzuk meg. A megoldásnak csak metsző alakzatokra kell helyes eredményt adnia.

Beküldendő egy tömörített i413.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.

(10 pont)

A beküldési határidő 2016. december 12-én LEJÁRT.

Megoldásokról:

A kevés beküldött megoldás közül egyetlen volt teljes értékű. Több versenyzőnél a paraméterek ellenőrzése (negatív sugár ne legyen), a cellák védelme maradt el.

Az egyenes ábrázolását érdemes -r és +r közé állítani, mert úgy megfelelő hosszúságú szakaszt látunk belőle. így a metszéspontokat is biztos látjuk.

Mintamegoldás:

Kis Lázár Bence 11. osztályos tanuló Dunaszerdahely, Magyar Tanítási Nyelvű Magángimnázium megoldása: i413.xlsx

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Kis Lázár Bence.
8 pontot kapott:	3 versenyző.
7 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2016. novemberi informatika feladatai