 |
Az I. 418. feladat (2017. január) |
I. 418. (É). A KML-2017 expedíció elsőként érkezett meg egy égitestre, hogy megállapítsa annak kéreghez közeli szerkezetét. Egy vizsgálat során a felszínen egy irányban haladva 500 méterenként megmérték a felszín alatti rétegek vastagságát. A műszer által detektált értékek megtalálhatók a retegek.txt állományban. A szöveges fájl első sorában a mérések száma (\(\displaystyle 2\le M\le 200\)), valamint a műszer által mért rétegek száma (\(\displaystyle 1\le R\le 20\)) szerepel. A további \(\displaystyle R\) sor mindegyikében \(\displaystyle M\) darab nemnegatív egész mutatja az egyes rétegek \(\displaystyle V_\text{mr}\) vastagságát (\(\displaystyle 0 \le V_\text{mr} \le 10\,000\)) méterben. A rétegek a felszíntől lefelé haladva vannak fölsorolva, a vastagság zérus értéke azt jelenti, hogy azon a mérési helyen az adott réteg teljesen elvékonyodott. Példaként vizsgáljuk meg a következő bemeneti állományt (a rövidebb írásmód kedvéért három sortörést / jellel helyettesítettünk), valamint a mérési eredmények alapján a felszín alatti rétegek egy lehetséges rajzát, ahol a mért értékeket szakaszokkal kötöttük össze.
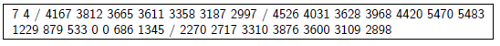
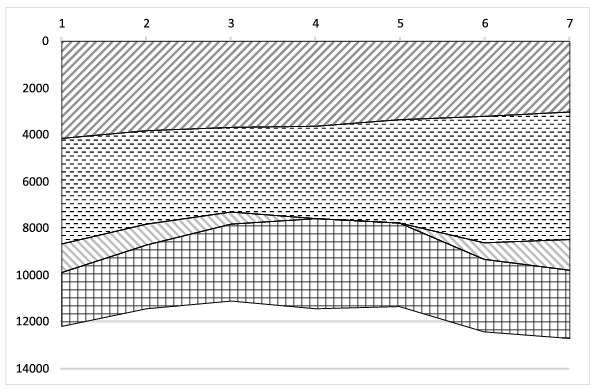
Készítsünk programot i418 néven, amely megoldja az alábbi feladatokat. A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk ki a feladat sorszámát (például 4. feladat:). A beolvasás előtt a várt tartalomra vonatkozó üzenetet jelenítsünk meg. Az ékezet nélküli kiírás is megengedett.
1. Olvassuk be és tároljuk a mérési eredményeket. Írjuk ki, hogy milyen hosszú úton végezte a csapat a mérést, illetve hány réteget rögzített a műszer.
2. Kérjük be egy réteg sorszámát, és adjuk meg, hogy az adott réteg hol és mekkora értékkel volt a legvastagabb és a legvékonyabb (pl. ,,A(z) 4. mérésnél volt a legvastagabb (3876 méter), és a(z) 1. mérésnél volt a legvékonyabb (2270 m) a(z) 4. réteg.'').
3. Állapítsuk meg, hogy hány réteg volt, amely a mérés során valahol teljesen elvékonyodott, és az eredményt írjuk ki (pl. ,,1 réteg vékonyodott el teljesen.'' vagy ,,Nem volt teljesen elvékonyodott réteg.'').
4. Számítsuk ki, hogy melyik mérési helyen, és a felszíntől milyen távol van a felszíntől legtávolabbi réteghatár (pl. ,,A(z) 7. mérési helyen 12723 méter mélyen van a legmélyebb feltérképezett réteghatár.'').
5. Kérjünk be egy mélység értéket (nemnegatív egész), és adjuk meg, hogy az egyes mérési pontokon a felszíntől számított hányadik rétegben van az adott mélység. Ha a távolság olyan nagy, hogy a mért rétegek alatt van, akkor a szám helyett egy kivonásjel kerüljön kiírása (pl. 9000 méterrel a felszín alatt az eredmény: 3 4 4 4 4 3 3).
6. Számoljuk meg, és írjuk ki, hogy hány olyan réteg van, amely a felszín valamely pontján is megjelenik (tehát az adott mérési helyen a felette lévő összes réteg vastagsága 0).
7. Előfordul, hogy egy réteg többször is eltűnik, de nem egymást követő mérési pontokon. Ilyenkor az adott rétegben ,,lencse'' alakul ki, amely el van zárva a saját rétege többi részétől. A felszínen nincsenek lencsék, tehát egy lencse minden pontja fölött kell lennie nem 0 vastagságú rétegnek. Keressük meg az ilyen lencséket, és írjuk ki mindegyik esetében, hogy hányadik rétegben található (azaz a lencse rétegének sorszámát), és legföljebb mekkora a hossza méterben mérve.
8. A mérési helyek között nem ismerjük a rétegek vastagságát és határvonaluk alakját, ezért két mérési hely között a rétegek határvonalát szakaszokkal helyettesítjük (ahogy a fenti ábrán). Ilyen módon minden réteg határvonala a kiindulási helytől számított bármely pontban megadható (a mérési helyeken pontosan, közöttük pedig a leírt közelítéssel). Számítsuk ki ezek alapján a kiindulási helytől számítva 100 méterenként, hogy az egyes rétegek középvonala a felszíntől mérve milyen mélységben halad. A réteg középvonala az adott helyen a felső és alsó határvonal számítani közepe. Az egész értékre kerekített értékeket a kozep.txt szöveges állományba írjuk ki. A fájl első sorában az indulási helytől mért távolságok szerepeljenek, majd a következő sorokban a rétegek középvonalai az adott helyen. Minden számérték között egy pontosvessző legyen a határoló jel.
Beküldendő egy tömörített i418.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Letölthető szöveges állományok:
retegek.txt, retegek2.txt, retegek3.txt.
(10 pont)
A beküldési határidő 2017. február 10-én LEJÁRT.
Mintamegoldásként Kis Lázár Bence 11. évfolyamos, dunaszerdahelyi versenyző munkáját adjuk közre: i418.cpp.
Statisztika:
4 dolgozat érkezett. 9 pontot kapott: Kis Lázár Bence. 8 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző.
A KöMaL 2017. januári informatika feladatai
