Az I. 449. feladat (2018. február)

I. 449. A helyi önkormányzati választásokon különböző szervezetek (nem feltétlenül csak pártok) indíthatnak jelölteket. A jelöltek egy része a választókerületekben méri össze népszerűségét, az lesz képviselő, aki a legtöbb szavazatot kapja.

Választási rendszerünkben azonban a többi jelöltre leadott szavazat sem vész kárba. Ezeket jelölőszervezetenként összeadják, az így kapott szám a jelölőszervezet ún. töredékszavazatainak száma. Minden jelölőszervezet készít egy ún. kompenzációs listát, ahonnan a kialakult töredékszavazatok számától függően a kiosztott mandátumok mellett még további képviselőket juttathat be az képviselőtestületbe. A töredékszavazatok alapján a mandátumok szétosztásáról a törvény a következőképpen rendelkezik:

\(\displaystyle a)\) Össze kell állítani egy táblázatot, amelyben minden lista neve alatt képezni kell egy számoszlopot. A számoszlop első száma az adott lista szavazatainak száma. A számoszlop következő számai az adott lista szavazatainak száma elosztva hárommal, öttel, héttel, rendre az új osztó az előző osztó kettővel megnövelt értéke.

\(\displaystyle b)\) Meg kell keresni a táblázatban előforduló legnagyobb számot, és amelyik lista számoszlopában találjuk meg azt, az a lista kap egy mandátumot. Ezt követően meg kell keresni a következő legnagyobb számot. Amelyik lista oszlopában találjuk, az a lista kap egy mandátumot. Ezt az eljárást kell folytatni mindaddig, míg kiosztásra kerül az összes mandátum.

(2010. évi L. törvény 15.§ (4))

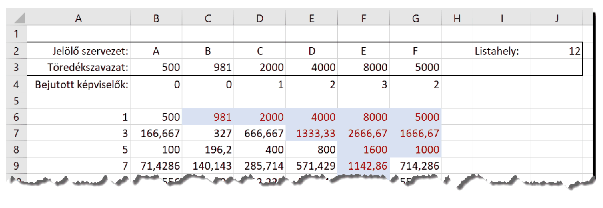
Feladatunkban tudjuk, hogy egy adott településen hat szervezet indított jelölteket (ezek legyenek rendre A, B, C, D, E és F). Ismerjük továbbá az egyes jelölőszervezetekre jutó töredékszavazatok számát és azt, hogy összesen hány további képviselő szerezhet mandátumot. (A mintán ezeket az adatokat a szegélyezett A2:J3 tartomány tartalmazza.)

Határozzuk meg a fenti számítási mód alapján, hogy az egyes jelölőszervezetek hány főt juttathatnak be a képviselőtestületbe a kompenzációs listájukról (a minta 4. sora). Feltételes formázással emeljük ki a táblázatban a mandátumot jelentő cellákat.

Beküldendő egy tömörített i449.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.

(10 pont)

A beküldési határidő 2018. március 12-én LEJÁRT.

Értékelés: A feladatra 10 megoldás érkezett, szinte minden helyes megoldás más alapötletre épül. Néhány versenyző esetén a J2-es cella tartalmától függetlenül mindig 12 bejutót ad vissza a munkalap. (Ők 5 vagy 6 pontot kaptak.) Egy beküldő makrókat alkalmazott. A feladat nem rendelkezett arról az esetről, amikor az osztószámok között van azonos, így ezt külön nem kellett vizsgálni. (A törvény ekkor így fogalmaz: "Ha a táblázatban előforduló legnagyobb szám keresésekor egyenlő legnagyobb számok vannak, akkor az a lista kap mandátumot, amelyik addig még nem szerzett mandátumot, vagy amelyik kevesebb mandátumot kapott, végezetül, amelyik a listasorsolásnál kisebb sorszámot kapott.")

Mintamegoldás: A mintamegoldás Szőnyi Laurának, a budapesti Baár-Madas Református Gimnázium 12. évfolyamos tanulójának dolgozata alapján készült, ez a megoldás volt a beküldött dolgozatok közül a legegyszerűbb. i449.xlsx

Statisztika:

10 dolgozat érkezett.
10 pontot kapott:	Békési Péter, Horcsin Bálint, Takács Árpád, Ürmössy Dorottya, Zsombó István.
9 pontot kapott:	Papp Marcell Miklós, Szőnyi Laura.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	2 versenyző.

A KöMaL 2018. februári informatika feladatai