Az I. 493. feladat (2019. november)

I. 493. Négyzet alakú mezőkből álló játéktereken, például táblás játékoknál vagy szimulációs programokban (lásd mintázatképződés, I.\(\displaystyle \;\)256. feladat) a szomszédság meghatározása lényeges.

Legyen adott egy \(\displaystyle N\times N\) (\(\displaystyle 5\le N\le 100\)) négyzetből álló játéktábla, amelynek minden mezője vagy üres, vagy egy bábut tartalmaz. A szomszédos mezők oldalaikkal vagy sarkaikkal érintkeznek, illetve a játéktér túlsó szélén vagy átellenes sarkán vannak. Két különböző mező \(\displaystyle T\) távolságban (\(\displaystyle 1\le T\le N/2\)) szomszédos, ha legföljebb \(\displaystyle T\) mezőn keresztül el lehet jutni az egyik mezőről a másikra. Például egy \(\displaystyle 6\times 6\)-os táblán a \(\displaystyle (2;2)\) mező 2 távolságú szomszédjai az ábrán szürke színezésűek.

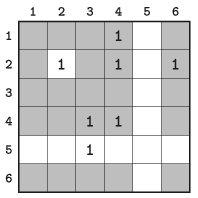
Készítsünk programot i493 néven, amely egy játéktábla pillanatnyi állása mellett megadja \(\displaystyle K\) darab kiválasztott mező \(\displaystyle T\) távolságú szomszédságában lévő mezőkön található bábuk számának összegét.

A program a standard bemenet első sorából olvassa be \(\displaystyle N\), \(\displaystyle K\) és \(\displaystyle T\) értékét, majd a következő \(\displaystyle N\) sorból soronként \(\displaystyle N\) darab egész számot: 1 vagy 0 jelöli, hogy az adott mezőn van bábu, vagy nincs. A következő \(\displaystyle K\) sorban a vizsgált mezők oszlop- és sor koordinátái szerepelnek. A program a standard kimenet első sorába írja a megadott \(\displaystyle K\) mező \(\displaystyle T\) távolságú szomszédságában található mezőkön lévő bábuk számának összegét.

Példa:

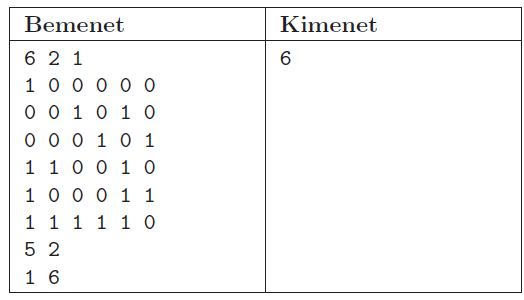
Beküldendő egy i493.zip tömörített állományban a program forráskódja és egy rövid leírás, ami megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

Letölthető állomány: beki.zip.

(10 pont)

A beküldési határidő 2019. december 10-én LEJÁRT.

Mintamegoldás: A közölt mintamegoldás Varga Balázstól, a dabreceni Debreceni Fazekas Mihály Gimnázium 11. osztályos tanulójától származik, és C++ nyelven készült: i493.cpp

Statisztika:

9 dolgozat érkezett.
10 pontot kapott:	Nagy 793 Márton, Varga 225 Balázs.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	2 versenyző.

A KöMaL 2019. novemberi informatika feladatai