Az I. 566. feladat (2022. május)

I. 566. (É). A 2022. januári számban megjelent I. 553. feladatban egy tízes számrendszerben adott számot kellett megadni faktoriális számrendszerben. A faktoriális számrendszerben megadott szám \(\displaystyle n\)-edik helyiértékén álló számjegyét \(\displaystyle n!\) értékével kell szorozni. Például a \(\displaystyle 235_{10}\) szám faktoriális számrendszerbeli alakja \(\displaystyle 14301_{!}\), azaz \(\displaystyle 1\cdot 1+3\cdot 6+4\cdot 24+1\cdot 120\). Amennyiben a faktoriális számrendszerben 9-esnél nagyobb számjegy fordul elő, akkor az ott szereplő számot zárójelbe tesszük. Például az \(\displaystyle 1(10)406010111_{!}\) szám második legmagasabb helyiértékű számjegye 10, és a szám tízes számrendszerben \(\displaystyle 77\,686\,689_{10}\).

Ebben a feladatban táblázatkezelő segítségével kell elkészítenünk az átváltást: egy faktoriális számrendszerben felírt egész szám tízes számrendszerbeli alakját kell megadni. A faktoriális számrendszerben felírt szám legföljebb 15 számjegyű, a nyitó és záró zárójelekkel együtt legföljebb 30 karakterből áll.

A megoldás során vegyük figyelembe a következőket:

\(\displaystyle \bullet\) Amennyiben lehetséges, és a feladat mást nem mond, akkor a megoldás során képletet, függvényt, hivatkozást használjunk.

\(\displaystyle \bullet\) A megoldáshoz segédszámításokat a K oszloptól jobbra végezhetünk.

\(\displaystyle \bullet\) A részfeladatok között van olyan, amely egy korábbi kérdés eredményét használja fel. Ha a korábbi részfeladatot nem sikerül teljesen megoldani, akkor használjuk a megoldását úgy, ahogy van, vagy helyettesítsük megfelelő értékkel, és azzal dolgozzunk tovább. Így ugyanis pontokat kaphatunk erre a részfeladatra is.

\(\displaystyle \bullet\) A megoldáshoz program vagy makró nem használható, kizárólag a  táblázatkezelő beépített függvényeivel dolgozzunk.

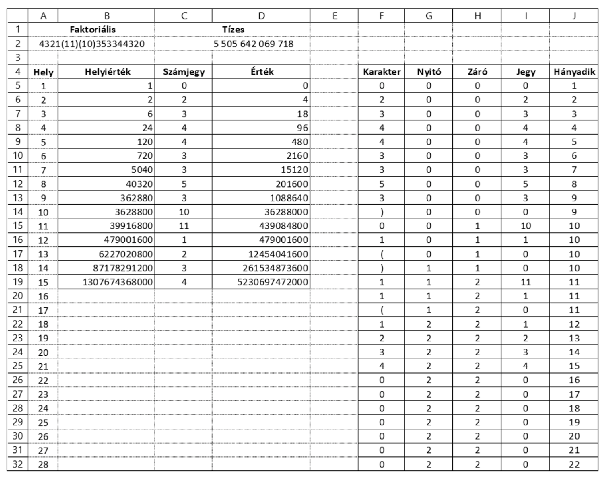
1. Alakítsuk ki a lenti mintának megfelelő táblázatszerkezetet és mentsük a táblázatot faktor10 néven a táblázatkezelő alapértelmezett formátumában.

2. Készítsük el az első és a negyedik sorban látott fejlécet, ahol szükséges egyesítsük a cellákat, illetve igazítsuk vízszintesen középre a cellák tartalmát.

3. Az A2 cellába írjunk be egy faktoriális számrendszerben megadott számot szövegként. A szám tízes számrendszerben adott alakja a C2-es cellában jelenjen meg.

4. Az A5:A34 tartományban adjuk meg az első 30 pozitív egész számot és a B5:B19 tartományban az első 15 egész szám faktoriálisát.

5. Az F5:F34 tartományban adjuk meg a B2 cellában található szöveg karaktereit egymás alatt úgy, hogy fentről lefelé a faktoriális számrendszerben adott szám karaktereit jobbról balra tudjuk kiolvasni. A szövegnél hosszabb karakterhelyeket jelölő cellákban 0 érték jelenjen meg.

6. A G5:G34 tartomány celláiban adjunk meg olyan képletet, amely megszámolja a faktoriális számban jobbról balra haladva az adott karakterhely előtt előforduló nyitó zárójeleket.

7. A H5:H34 tartomány celláiban adjunk meg olyan képletet, amely megszámolja a faktoriális számban jobbról balra haladva az adott karakterhely előtt előforduló záró zárójeleket.

8. Az I5:I34 tartomány celláiban határozzuk meg a faktoriális szám megfelelő számjegyét. A zárójeleket tartalmazó sorokban 0 értéket adjunk meg vagy hagyjuk üresen, a nyitó és záró zárójelek közötti sorokban állítsuk elő a többjegyű szám számjegyei alapján a többjegyű szám értékét, ami az utolsó zárójelen belüli szám sorában jelenjen meg.

9. A J5:J34 tartomány celláiban adjuk meg, hogy az előző oszlopban szereplő számjegy a kisebb helyiértékektől indulva hányadik számjegye a faktoriális számrendszerbeli számnak. Amennyiben az I oszlopban nem egy számjegy értéke van, akkor ott az előző sorban lévő számot adjuk meg. Egy szám a minta szerint többször is megjelenhet, de sorrendben az első szám adja meg, hogy az adott sorban az I oszlopban kapott érték hányadik számjegyét adja a faktoriális számrendszerbeli számnak.

10. A C5:C19 tartományban adjuk meg a J oszlopban meghatározott sorszám alapján a faktoriális számrendszerbeli szám megfelelő helyiértékén álló számjegyet tízes számrendszerben, vagy 0 értéket.

11. A D5:D19 tartományban adjuk meg a B és C oszlopban lévő megfelelő értékek szorzatát, vagy 0 értéket.

12. A C2 cellában adjuk meg a D5:D19 tartományban kiszámított számok összegét.

13. Formázzuk a táblázatot a mintának megfelelően.

Minta:

Beküldendő egy tömörített i566.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.

(10 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Statisztika:

4 dolgozat érkezett.
10 pontot kapott:	Gyönki Dominik, Hinek Milán, Nagy 292 Korina, Vadász Levente Márton.

A KöMaL 2022. májusi informatika feladatai