Az I. 572. feladat (2022. október)

I. 572. Sok sportág lebonyolítási formája részben, vagy teljesen körmérkőzéses rendszerben történik. Az ilyen versenyek során minden résztvevő az összes többi résztvevővel egyszer megmérkőzik.

Készítsük el \(\displaystyle n=8\) résztvevőre a körmérkőzés párosításait táblázatkezelő alkalmazás segítségével a minta alapján. A mintán látható sárga mezőkbe szabad a csapatneveket begépelni, a többi cella értékét függvényekkel állítsuk elő. A megoldás annál több pontot ér, minél több a függvények között a másolható.

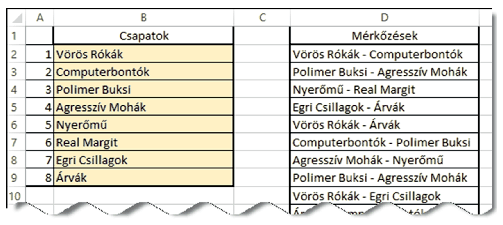
A táblázat szerkezetét, a cellák formázását állítsuk be a minta szerint. Ügyeljünk a megfelelő cellák szélességére, szegélyezésére és a tartalom igazítására. Segédszámításokat végezhetünk az E oszloptól jobbra, amelyek értelmezését feliratokkal segítsük elő vagy a dokumentációban írjuk le. A megoldásban saját függvény vagy makró nem használható.

Beküldendő egy tömörített i572.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.

(10 pont)

A beküldési határidő 2022. november 15-én LEJÁRT.

Mintamegoldás:

Vadász Horváth Milán a pécsi, PTE Gyakorló Általános Iskola, Gimnázium és Óvoda, 12. osztályos tanulójától származik: I572.xlsx

Magyarázata:

Az L1:T9 tartományt a megoldás szemléltetésére használom csak, annak a számításokban semmilyen szerepe sincs.

A körmérkőzés párosítását úgy képzelem el, mintha egy 8x8-as mátrixnak az egyik fele lenne, az átlóját nem beleértve. Ilyenkor megvalósul, hogy a metszéspontokban mindenki mindenkivel pontosan egyszer találkozik. Ezt a "félmátrixot" szemlélteti az L1:T9 tartomány.

Az F és G oszlopokban történik a függvényekkel való számolás. Konkrét értékként csak az F2 cellában lévő 1-es van megadva, a többi értékek kiszámítása mind függvényekkel valósul meg. A G oszlop celláinak értéke attól függ, hogy a balra melletük lévő cella értéke megegyezik-e a felette lévőével. Ha nem egyezik meg, akkor az azt jelenti, hogy az F-ben úgymond új szakaszhoz értünk, tehát a G oszlop adott cellájának értéke az F oszlop adott cellája feletti cellájának értékénél 1-el többel kell, hogy legyen. Ha megegyezik, akkor az azt jelenti, hogy egy adott számon haladunk tovább az F oszlopban azaz a G oszlop adott cellájának értéke 1-el kell, hogy több legyen, mint a felette lévő cellában lévő érték. Az F oszlop celláiban történik annak az ellenőrzése, hogy a G oszlop jobbra fel szomszédos cellájának értéke 8-e. Ha igen, akkor az F oszlop adott cellájának értéke már 1-el több lesz mint a felette lévő, ha nem akkor, a felette lévővel fog megegyezni az értéke. Ezen elvek szerint megírtam a függvényeket, majd "végighúztam" azokat. Így megkaptam az összes lehetséges, 28 darab párosítást. (Ennek értékét matematikai tekintetben binomiális együtthatóval ellenőriztem 8 alatt a 2-re vonatkoztatva)

Ezután már csak az van hátra, hogy a D oszlopban az F és G oszlop számai szerint a csapatok neveivel jelenjenek meg a párosítások. Ehhez az FKERES és a SZÖVEGÖSSZEFŰZÉS függvényeket használtam.

Statisztika:

18 dolgozat érkezett.
10 pontot kapott:	Gyönki Dominik, Hinek Milán, Horváth Milán, Nagy 292 Korina, Szabó Imre Bence, Vadász Levente Márton.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2022. októberi informatika feladatai