 |
Az I. 599. feladat (2023. október) |
I. 599. Egy számsorozatot akkor nevezzünk Fibonacci-típusúnak, ha a harmadiktól kezdve mindegyik eleme az előző kettő összege. A sorozat legismertebb formája, ha az első két szám 0 és 1.
A sorozatot rekurzióval definiáljuk, amit iteratív módon is könnyen kódolni tudunk.
$$\begin{align*} \tag{1} F_{0}& = 0, \qquad F_{1} = 1;\\\tag{2} F_{n+1} & = F_{n-1} + F_{n} \quad (n\ge 1). \end{align*}$$
A sorozat elemei gyorsan növekednek. Változtassuk meg a 2. képletet.
\(\displaystyle \tag{3} F_{n+1} = (F_{n-1} + F_{n}) \mod m \quad (n\ge 1). \)
A képletben szereplő \(\displaystyle m\) (\(\displaystyle m> 1\)) egész szám, amellyel a sorozat új elemét maradékosan osztjuk. A sorozat periodikus, előbb-utóbb újra szerepel benne 0 és 1, így ismétlődni kezdenek az értékek.
Készítsünk programot, amely \(\displaystyle m\) értékét beolvassa és a képernyőre kiírja a periódus hosszát, valamint egy új sorba a periódus elemeit.
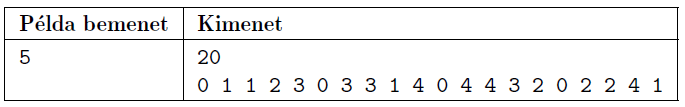
Beküldendő egy tömörített i599.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2023. november 15-én LEJÁRT.
Minta megoldások:
Demcsák Patrik a budapesti Sztehlo Gábor Evangélikus Óvoda, Általános Iskola és Gimnázium 10. osztályos tanulójának munkája: I599.py
Pál Benedek József szegedi Radnóti Miklós Kísérleti Gimnázium 12- osztályos tanulójának munkája: i599.cpp
Statisztika:
31 dolgozat érkezett. 10 pontot kapott: Anastasiia Nosyk, Bátorfi Balázs, Bürger Ádám, Csíkos 256 Benjamin, Debreczeni Huba, Demcsák Patrik, Dömők Bernadett, Gincsai Gábor, Gyönki Dominik, Hajdufi Hunor, Hajós-Szabó Máté, Halmosi Dávid, Hegyi Benedek, Illés Gergely Levente, Nagy 292 Korina, Oláh Barnabás, Pál Benedek József , Pisaru Tomas, Puppi Barna, Rózsa Zsombor, Schmidt Marcell, Simon-Hajdú Gergő, Sógor-Jász Soma, Szabó Imre Bence, Váróczi Ákos Mihály, Viszkocsil Norton. 9 pontot kapott: Kézeli Dominik, Nuyen Ádám. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2023. októberi informatika feladatai
