 |
Az I. 601. feladat (2023. október) |
I. 601. 1777-ben George Louis Leclerc, Buffon grófja vetette fel a ,,tűprobléma'' néven ismert feladatot: Mekkora a valószínűsége annak, hogy \(\displaystyle k\) hosszúságú tűt dobva a \(\displaystyle d\) szélességű lapokból álló padlóra, a leeső tű metszi a padlólapok közti egyik vonalat?
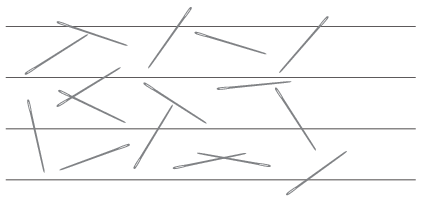
Nézzük ennek a matematikai megközelítését!
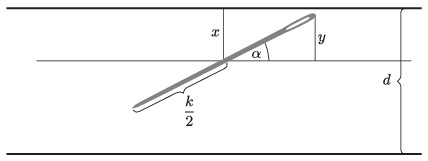
Jelölje \(\displaystyle x\) a tű középpontjának a legközelebbi vonaltól mért távolságát \(\displaystyle \left(0 \le x \le \frac{d}{2}\right)\).
Legyen a tű és a padló vonalainak szöge \(\displaystyle \alpha\) \(\displaystyle (0^\circ \le \alpha < 180^\circ)\).
Ekkor a tű vége \(\displaystyle y\) értékkel kerül magasabbra a tű középpontjánál \(\displaystyle \bigg(\sin \alpha = \frac{y}{\frac{k}{2}}\), vagyis \(\displaystyle y = \frac{k}{2} \cdot \sin\alpha\bigg)\). Ha \(\displaystyle y < x\), akkor nem metszi a tű a vonalat.
Annak az esélye, hogy metszi a tű a padlóvonalat: \(\displaystyle p = \frac{2}{\pi} \cdot \frac{k}{d}\), ezért a kísérlet a \(\displaystyle \pi\) meghatározására is használható.
Az előző képletből \(\displaystyle \pi\)-t kifejezve: \(\displaystyle \pi = \frac{2k}{pd}\).
Szimuláljuk a kísérletet számítógéppel. Hat különböző \(\displaystyle k\) és \(\displaystyle d\) értékre végeztessünk a táblázatkezelővel \(\displaystyle 10\,000\,--\,10\,000\) dobáskísérletet, majd mindegyiknél határozzuk meg a \(\displaystyle p\) relatív gyakoriságát. Ezekből kapunk hat becslést a \(\displaystyle \pi\) értékére, majd ezeket átlagoljuk.
1. Nyissunk meg egy üres táblázatkezelő munkafüzetet, majd mentsük buffontu néven.
2. Hozzuk létre és formázzuk a minták szerinti elrendezést.
3. Gépeljük be a szöveges adatokat az A1:A4 és a B5:S5 tartományokba, alkalmazzunk ezekre a cellákra félkövér betűstílust. Az A6:A1005 tartományba kerüljenek az \(\displaystyle 1, 2, \ldots, 999, 1000\) értékek. A C, az F, az I, az L, az O és az R oszlopok első két sorába gépeljük be a mintákon látható, \(\displaystyle k\) és \(\displaystyle d\) aktuális értékére vonatkozó adatokat.
4. Szegélyezzük a táblázat celláit a minta szerint, a rácsozás az 1005. sorig tartson.
5. A B, az E, a H, a K, az N és a P oszlopok 6\(\displaystyle \,\)–\(\displaystyle \,\)1005. sorába kerüljön olyan képlet, amely a véletlenszám generátor segítségével megad egy 0 és \(\displaystyle \frac{d}{2}\) közötti értéket. Az adat négy tizedesjegy pontossággal jelenjen meg.
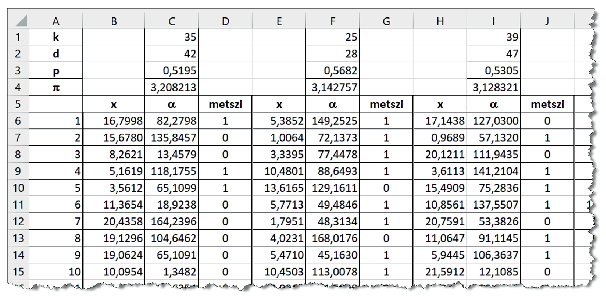
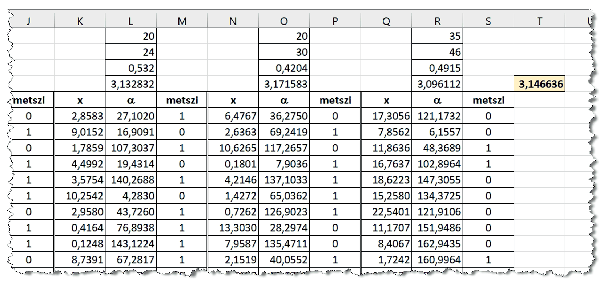
6. A C, az F, az I, az L, az O és az R oszlopok 6\(\displaystyle \,\)–\(\displaystyle \,\)1005. sorába kerüljön olyan képlet, amely véletlenszám generátor segítségével megad egy \(\displaystyle 0^\circ\) és \(\displaystyle 180^\circ\) közötti szögértéket. Az adat két tizedesjegy pontossággal jelenjen meg.
7. A D, a G, a J, az M, a P és az S oszlopok 6\(\displaystyle \,\)–\(\displaystyle \,\)1005. sorába kerüljön 0, ha a tű nem metszi a vonalat, vagyis \(\displaystyle y < x\); ellenkező esetben a cella értéke legyen 1.
8. A C3, az F3, az I3, az L3, az O3 és az R3 cellákban szerepeljen olyan képlet, amely megadja a ,,metszés'' adott tesztben mért relatív gyakoriságát \(\displaystyle \left(\frac{\text{jó esetek száma}}{\text{kísérletek száma}}\right)\).
9. A C4, az F4, az I4, az L4, az O4 és az R4 cellákban az a képlet szerepeljen, amely megadja a \(\displaystyle \pi\) értékére kapott becslést az adott tesztben.
10. Végül átlagoljuk ezek értékét a T4 cellában. Állítsuk be a cella jellemzőit a mintán láthatóra.
Segédszámításokat az U oszloptól jobbra végezhetünk. A megoldásban saját függvény vagy makró nem használható.
Beküldendő egy tömörített i601.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
A beküldési határidő 2023. november 15-én LEJÁRT.
Statisztika:
23 dolgozat érkezett. 10 pontot kapott: Pál Benedek József , Puppi Barna, Szabó Attila-Zsolt, Szabó Imre Bence, Viszkocsil Norton. 9 pontot kapott: Bátorfi Balázs, Bődi Marcell, Dely Bendegúz, Gyönki Dominik, Halmosi Dávid, Oláh Barnabás, Schmidt Marcell, Sógor-Jász Soma. 8 pontot kapott: 2 versenyző. 7 pontot kapott: 5 versenyző. 6 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2023. októberi informatika feladatai
