 |
Az I. 605. feladat (2023. november) |
I. 605. Adott egy 500 mm oldalhosszú négyzet alakú terület 1000 mm magas kerettel körülvéve. A területen létrehoztak egy felszínt, amelyik sehol nem haladja meg a keret magasságát. A terület rácspontjaiban pici csapágygolyót tehetünk a felületre és vizsgálhatjuk, hogy mi történik vele. Lehet, hogy nem mozdul, de az is lehet, hogy a kiindulási helyéről legurul.
A golyó akkor marad egy rácspontban, ha a helyét körülvevő nyolc rácspont egyikében sem kisebb a felszín magassága az aktuálisnál. A golyó akkor gurul át valamelyik szomszéd rácspontba, ha ott a felszín magassága kisebb, mint az eredeti pontban. Ha több irányba is gurulhatna, akkor a legnagyobb meredekségű irányt választja, vagyis azt a szomszéd mezőt, ahol a legkisebb magasságérték van. Ha több ilyen magasságú szomszéd van, akkor a táblázat szerint a legkisebb sorszámú szomszéd irányt választja.
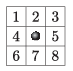
Készítsük el a golyó mozgását szimuláló táblázatkezelő munkafüzetet.
1. Nyissunk meg egy üres munkafüzetet és mentsük golyo néven a program alapértelmezett formátumában. Legyen a munkalap neve Terep.
2. Illesszük be a munkalapra a B2 cellától kezdődően a tabulátorokkal tagolt, UTF-8 kódolású terep.txt fájl tartalmát.
3. Gépeljük be az A1 cellába a mintán látható szöveget, a minta szerint illesszük be a sorszámokat 1-től 502-ig az első sor és oszlop megfelelő celláiba, majd formázzuk meg ezeket a minta szerint.
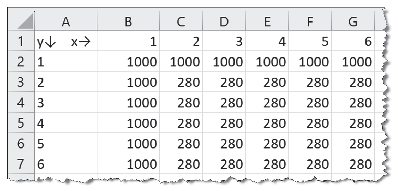
4. Hozzuk létre a munkafüzetben a Mozgás nevű munkalapot, majd végezzük el a következőket:
\(\displaystyle a.\) Gépeljük be és formázzuk meg a minta szerint az első két sor celláit.
\(\displaystyle b.\) Állítsuk be, hogy a C1 és az E1 cellába csak 2 és 501 közötti egész számokat lehessen begépelni, ha más adatot próbálunk meg ezekbe a cellákba írni, hibaüzenet figyelmeztessen.
\(\displaystyle c.\) Az A3 cellától kezdődően jelenjen meg a sorszám 0-tól indítva, mellettük a B, C és D oszlopban jelenjen meg a golyó aktuális helyzete \(\displaystyle (x,y)\) és a terep magassága \(\displaystyle (h)\) ebben a rácspontban.
\(\displaystyle d.\) A következő sorban jelenjenek meg annak a szomszédos pontnak az adatai, ahová a golyó átgurul, ha van ilyen, és maradjanak üresek a cellák, ha a golyó megáll.
\(\displaystyle e.\) Készítsük fel a táblát 1000 lépés vizsgálatára, de adatok csak addig a sorig jelenjenek meg, amíg a golyó mozog.
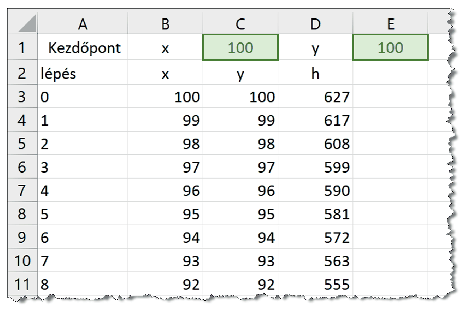
5. Készítsük el a terep \(\displaystyle (400;202)\) pontjára kerülő golyó útjáról a mintákon látható ponttípusú diagramot és grafikont.
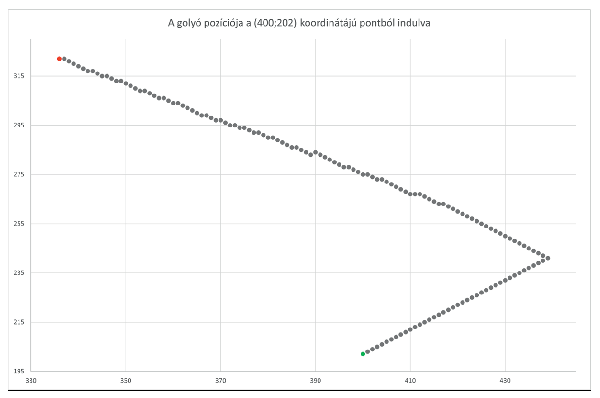
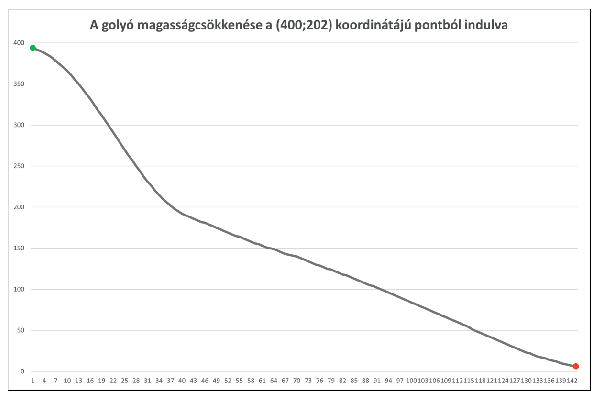
\(\displaystyle a.\) A diagramok kerüljenek a Pozíció és Magasság nevű, új munkalapokra.
\(\displaystyle b.\) Formázzuk a diagramokat a minták szerint. A kezdőpont és a végpont jelölése mindkettőn legyen zöld, illetve piros.
Segédszámításokat a Mozgás munkalap E oszlopától jobbra végezhetünk. A megoldásban saját függvény vagy makró nem használható.
Beküldendő egy tömörített i605.zip állományban a táblázatkezelő munkafüzet (golyo.xlsx, golyo.ods, ...), illetve egy rövid dokumentáció (golyo.txt, golyo.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
A megoldáshoz szükséges letölthető állomány: terep.txt.
(10 pont)
A beküldési határidő 2023. december 15-én LEJÁRT.
Statisztika:
21 dolgozat érkezett. 10 pontot kapott: Gyönki Dominik, Nagy 292 Korina. 9 pontot kapott: Bátorfi Balázs, Halmosi Dávid, Puppi Barna, Schmidt Marcell, Sógor-Jász Soma. 8 pontot kapott: 1 versenyző. 7 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 3 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2023. novemberi informatika feladatai
