A K/C. 822. feladat (2024. szeptember)

K/C. 822. Kati azt a feladatot kapta, hogy számítsa ki a mellékelt ábrán látható körbe rajzolt ötszög területét. Az oldalak hosszát cm-ben mérve az ábrán jelölték. Kati elvégezte a számításokat, és \(\displaystyle {30+10{,}5\sqrt{30}~\mathrm{cm}^2}\) jött ki neki eredményül. Jól szá­molt-e Kati?

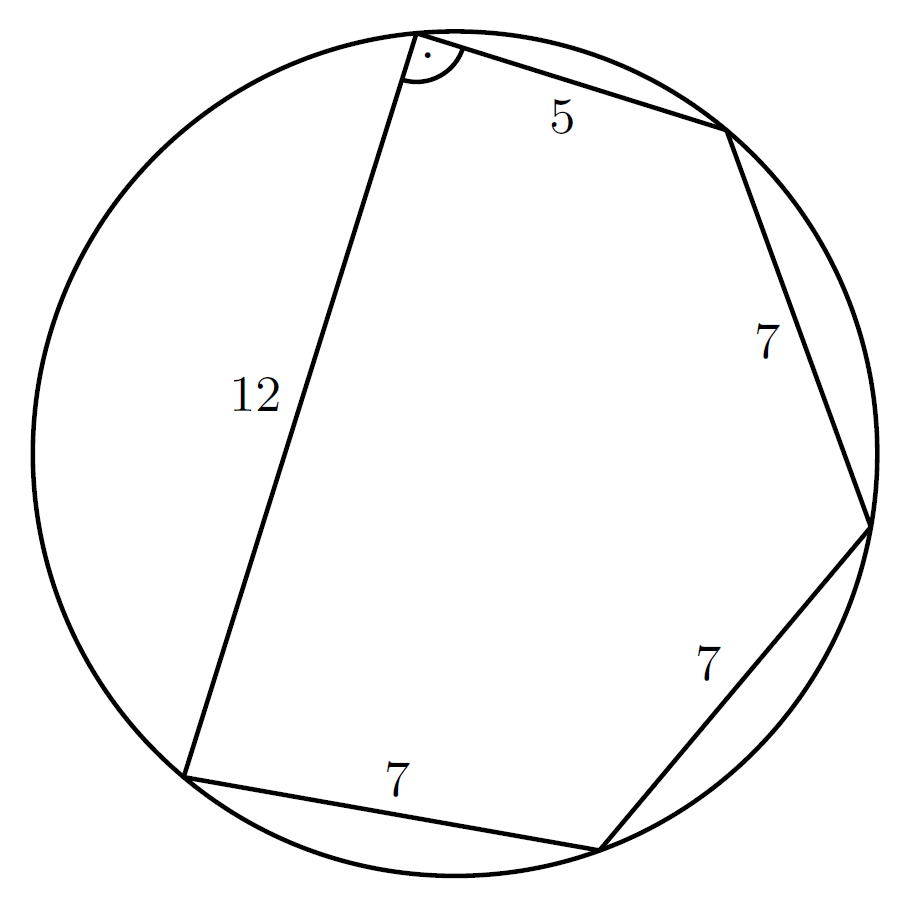
(5 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás. Kati nem számolhatott jól, ugyanis a feladatban szereplő adatokkal rendelkező ötszög nem létezik.

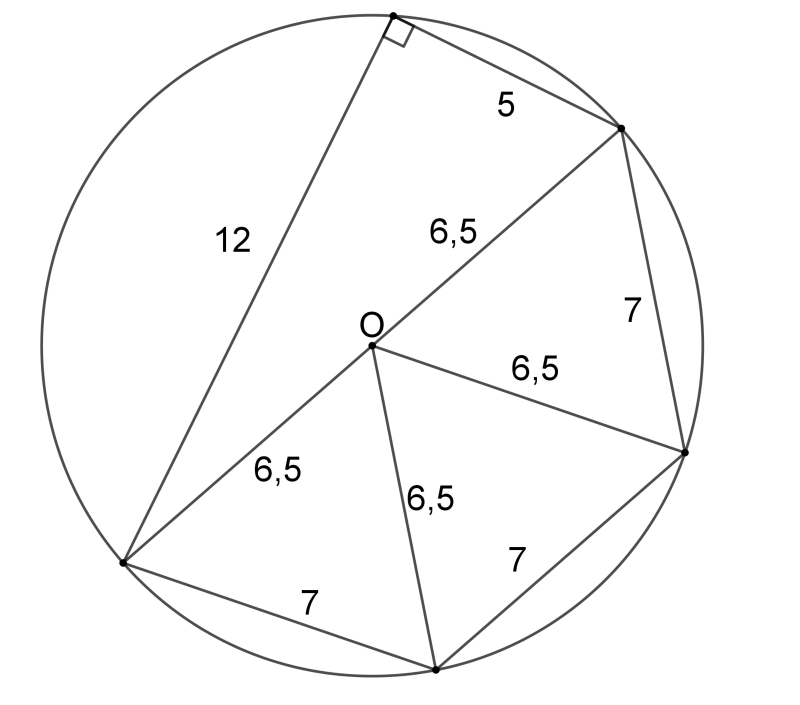
Az \(\displaystyle AC\) a \(\displaystyle B\)-nél levő derékszög miatt 13 cm hosszú, és a Thalész-tétel megfordítása miatt egyben a kör átmérője. A kör sugara így 6,5 cm. Az \(\displaystyle OCD\), \(\displaystyle ODE\) és \(\displaystyle OEA\) háromszögek egybevágók, ezért az \(\displaystyle O\)-nál levő szögük 60 fokos, ekkor viszont, mivel egyenlő szárúak, szabályos háromszögek. Így a 7 cm hosszúnak jelölt oldalak hossza csak 6,5 cm lehetne, tehát az ábrán látható \(\displaystyle AEDCB\) ötszög ezekkel az adatokkal nem létezik.

Statisztika:

307 dolgozat érkezett.
5 pontot kapott:	Araguas Mátyás, Bara Boglárka , Barta Zsófia, Bloemsma Péter Sándor, Bodó Rókus Dániel, Chen Zhibo, Dornbach Bernadett, Farkas Noémi , Fehér Ádám, Feith Benedek, Halász Tamás, Kapiller Ákos Péter, Kerekes 333 Zoltán, Kolencsik Nándor, Kóródy Vera, Kothencz Luca, Kovács 444 Kamilla, Kovács Dorka Sára, Kudomrák Lili Anna , Kun Milán, Kun Petra, Li Mingdao, Márfai Lili, Maróti Olga, Mateas Isabelle, Molnár Levente, Patócs 420 Péter, Pázmándi Renáta , Péter Tamás, Piller Zsófia, Pivárcsik Márk, Pocsay Bence Máté, Poczai Dorottya, Radošická Emma, Rózsa Péter, Sajó Marcell 16, Szabados Ákos, Szabó Máté, Szalóki Árpád, Szathmáry Zalán, Szedmák Szabrina, Szélpál Botond, Szighardt Anna, Tófalvy Máté, Tóth Luca, Válek Péter, Viczián Adél.
4 pontot kapott:	15 versenyző.
3 pontot kapott:	33 versenyző.
2 pontot kapott:	40 versenyző.
1 pontot kapott:	86 versenyző.
0 pontot kapott:	17 versenyző.
Nem versenyszerű:	7 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	54 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai