A K. 108. feladat (2006. december)

K. 108. Egy 100 m oldalhosszúságú, négyzet alakú füvesített teret a határvonala mentén kövezett járda vesz körbe. Az emberek leggyakrabban a négyzet alakú terület A sarkától a szemközti oldal F felezőpontjába szeretnének eljutni. Ezt úgy is megtehetik, hogy a terület határa mentén a kövezett járdán közlekednek az ABF útvonalon, de néhányan gyalogutat alakítottak ki a füvön keresztül úgy, hogy elindultak az AB oldal mentén, majd egyenesen átvágtak a téren F felé, az ábrán látható módon. Így a határ mentén megtett úthoz képest 25%-kal kevesebb utat kell megtenniük. Milyen messze van az A ponttól a füvön keresztül vezető gyalogút K kezdőpontja?

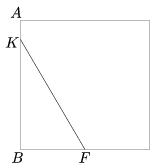
(6 pont)

A beküldési határidő 2007. január 10-én LEJÁRT.

Megoldás. Jelölje AK hosszát x, ekkor KB=100-x. A Pitagorasz-tétel segítségével felírhatjuk a gyalogutat használók által megtett távolságot: . Ez a mondottak értelmében 25%-kal kevesebb, mint az ABF útvonal hossza, ami 150 m. Ennek megfelelően . Átrendezve és négyzetre emelve (100-x)²+50²=(112,5-x)². A zárójeleket felbontva x² kiesik, a kapott elsőfokú egyenletből x=6,25. Tehát a gyalogút az A ponttól 6,25 m-re indul.

Megjegyzés: Néhányan csodálkozhatnak, hogy miért nem rögtön az A pontból indul el az átvágás, miért kell az AB oldal mentén haladni még egy kicsit. A feladat az életből vett példa, az ELTE (Eötvös Loránd Tudományegyetem) matematika és fizika épülete közti téren valamilyen furcsa oknál fogva a feladatban megadott módon alakult ki az átlós gyalogút. A mellékelt fényképfelvételen ez látható.

Statisztika:

156 dolgozat érkezett.
6 pontot kapott:	88 versenyző.
5 pontot kapott:	42 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2006. decemberi matematika feladatai