A K. 117. feladat (2007. február)

K. 117. Egy lapot az ábrának megfelelően a szaggatott vonalak mentén harmadára hajtjuk (mindkét hajtás tetszőleges ,,irányú'' lehet). A hajtásvonalak a lap két oldalát összesen hat részre osztják. Széthajtogatás után a hat rész mindegyikét különböző színűre színezzük, majd az eredeti hajtás mentén ismét összehajtjuk a lapot. Így csak két szín fog látszani, a két fedőlapon. Hány különböző színpárosítás valósítható meg különböző hajtogatásokkal?

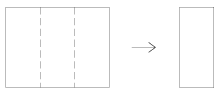
(6 pont)

A beküldési határidő 2007. március 16-án LEJÁRT.

Megoldás. Minden résznek két másik lehet a párja (1-esnek 2-es és 6-os; 2-esnek 1-es és 3-as; 3-asnak 2-es és 4-es, 4-esnek 5-ös és 3-as, 5-ösnek 4-es és 6-os, 6-osnak 1-es és 5-ös), ez összesen 12 lehetséges pár, de mindegyiket mindkettőnél megszámoltuk, így ennek fele, azaz 6 lehetséges színpárosítás van.

Statisztika:

137 dolgozat érkezett.
6 pontot kapott:	100 versenyző.
5 pontot kapott:	23 versenyző.
4 pontot kapott:	4 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2007. februári matematika feladatai