Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A K. 155. feladat (2008. január)

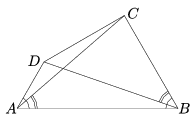
K. 155. Az ábrán látható négyszögben

DAB\sphericalangle = ABC\sphericalangle =60^\circ,

valamint CAB\sphericalangle =CBD\sphericalangle. Bizonyítsuk be, hogy AD+CB=AB.

(6 pont)

A beküldési határidő 2008. február 11-én LEJÁRT.

Megoldás. Az AD és CB oldalakat meghosszabbítva egy szabályos háromszöget kapunk. Az ABC háromszög és az EDB háromszög egybevágó, hiszen AB=EB és a három szögük is megegyezik. A két háromszög egybevágóságából következik, hogy megfelelő oldalai egyenlők, azaz CB=DE, így AD+CB=AD+DE=AE=AB.

Statisztika:

128 dolgozat érkezett.
6 pontot kapott:70 versenyző.
5 pontot kapott:22 versenyző.
4 pontot kapott:10 versenyző.
3 pontot kapott:3 versenyző.
2 pontot kapott:7 versenyző.
1 pontot kapott:9 versenyző.
0 pontot kapott:6 versenyző.
Nem versenyszerű:1 dolgozat.

A KöMaL 2008. januári matematika feladatai