Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A K. 156. feladat (2008. január)

K. 156. A körben lévő házikó alja négyzet, teteje szabályos háromszög. Bizonyítsuk be, hogy a ház oldalának hossza a kör sugarával egyezik meg.

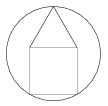
(6 pont)

A beküldési határidő 2008. február 11-én LEJÁRT.

Megoldás. Kössük össze a kör középpontjával a ház E csúcsát, és B sarkát.

CB=CD=EC, tehát az ECB háromszög egyenlő szárú, alapon fekvő szögei egyenlőek, nagyságuk pedig: BEC\angle=EBC\angle=\frac{180^{\circ}-ECB\angle}{2}=\frac{180^{\circ}-(60^{\circ}+90^{\circ})}{2}=15^{\circ}.

EO=OB=r, így az EOB_{\triangle} egyenlő szárú, és így alapon fekvő szögei egyenlőek: OBE\angle=OEB\angle=OEC\angle-BEC\angle=\frac{60^{\circ}}{2}-BEC\angle=30^{\circ}-15^{\circ}=15^{\circ}. (Felhasználtuk, hogy EO felezi a DEC\angle-et.)

EOB_{\triangle} egybevágó az ECB_{\triangle}-gel, hiszen alapjuk és az azon fekvő szögek egyenlőek. Ennélfogva száraik is egyenlő hosszúak, vagyis a kör sugara megegyezik a ház oldalával.

Statisztika:

125 dolgozat érkezett.
6 pontot kapott:60 versenyző.
5 pontot kapott:13 versenyző.
4 pontot kapott:7 versenyző.
3 pontot kapott:5 versenyző.
2 pontot kapott:9 versenyző.
1 pontot kapott:14 versenyző.
0 pontot kapott:16 versenyző.
Nem versenyszerű:1 dolgozat.

A KöMaL 2008. januári matematika feladatai