A K. 191. feladat (2008. december)

K. 191. Kétféle ablaktörlőt vizsgálunk, mindkettőnél a 31 cm-es törlőlapát a közepénél egy szintén 31 cm hosszú nyélre van rögzítve, amelyik egy tengely körül 90^o-ot fordul törlés közben. Az első típusnál a rögzítés fix, így a törlő kezdetben 45^o-ot zár be az ablak aljával, és törlés közben a lapát mindig a nyél irányába mutat. A másik típusnál a rögzítésnél csukló van, így a törlő végig merőleges az ablak aljára a törlés alatt. Melyik típusú ablaktörlő töröl le nagyobb területet?

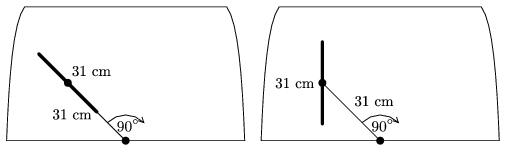
(6 pont)

A beküldési határidő 2009. január 10-én LEJÁRT.

Megoldás. Az első típusnál egy negyed körgyűrűről van szó, aminek területe .

A másik típusnál létrejövő alakzatot a végig az ablak aljával párhuzamosan mozgó ablaktörlőlapát két végső állása és a rögzítési pont által leírt negyed körívvel azonos körívek határolják. Ha ennek felső körszeletét levágjuk, az pont az alsó körszeletbe illik, létrehozva egy az eredeti alakzattal megegyező területű téglalapot. A téglalap egyik oldala 31 cm, a másik a 31 cm befogójú egyenlőszárú derékszögű háromszög átfogójával egyezik meg. Ennek hossza , így a téglalap területe 1359 cm². Tehát ez a fajta megoldás kevesebb területet tisztít meg.

Statisztika:

180 dolgozat érkezett.
6 pontot kapott:	Bereczki Ferenc, Borbély Roland, Böröndy Áron, Fazekas Gábor László, Halász 423 Dániel, Kaposi Ágoston, Kasó Márton, Katona Bálint, Kis Attila Soma, Kővágó Zoltán, Nagy 014 Gergely, Pácsonyi Márton, Reskó Sándor, Straubinger Dániel, Szigeti Bertalan György, Szőts Nóra, Tolnai Dániel, Wiszt Attila, Zagyva Dániel.
5 pontot kapott:	70 versenyző.
4 pontot kapott:	25 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	20 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	9 versenyző.
Nem versenyszerű:	8 dolgozat.

A KöMaL 2008. decemberi matematika feladatai