Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A K. 204. feladat (2009. február)

K. 204. Az alábbi ábrát akarjuk elkészíteni. Mennyi lesz a satírozott terület és a nem satírozott terület aránya? (Az ábrát határoló görbék félkörök, az átmérőn látható pontok harmadolópontok.)

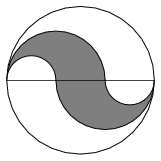
(6 pont)

A beküldési határidő 2009. március 10-én LEJÁRT.

Megoldás. Az ábra alsó felét a legnagyobb félkör függőleges szimmetriatengelyére tükrözve az alábbi ábrához jutunk:

A legkisebb kör sugarát jelölje r.

A legnagyobb kör területe: (3r)² $\pi$ =9r² $\pi$ .

A középső "félhold" - a satírozott rész - területe:

(2r)² $\pi$ -r² $\pi$ =3r² $\pi$ .

A nem satírozott rész területe: 9r² $\pi$ -3r² $\pi$ =6r² $\pi$ .

A kérdéses arány tehát:

$\frac{3r^2\pi}{6r^2\pi}=\frac12.$

Statisztika:

167 dolgozat érkezett.

6 pontot kapott: 97 versenyző.

5 pontot kapott: 25 versenyző.

4 pontot kapott: 14 versenyző.

3 pontot kapott: 9 versenyző.

2 pontot kapott: 6 versenyző.

1 pontot kapott: 1 versenyző.

0 pontot kapott: 4 versenyző.

Nem versenyszerű: 11 dolgozat.

A KöMaL 2009. februári matematika feladatai

167 dolgozat érkezett.
6 pontot kapott:	97 versenyző.
5 pontot kapott:	25 versenyző.
4 pontot kapott:	14 versenyző.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	11 dolgozat.