A K. 248. feladat (2010. március)

K. 248. Az ábrán egy kocka hálóját látjuk. Fessünk be a kockaháló hat négyzete közül kettőt pirosra, a másik négy közül pedig egyet-egyet fehérre, zöldre, sárgára és kékre úgy, hogy a majd ebből elkészített kockának ne legyen két szomszédos oldala azonos színű.

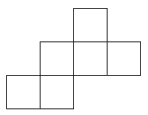
Hányféleképpen színezhetjük az ábrát eme feltételeknek megfelelően?

(6 pont)

A beküldési határidő 2010. április 12-én LEJÁRT.

Megoldás. Számozzuk meg a négyzeteket!

Az összehajtás után az 1-nek a 6, a 6-nak az 1 kivételével mindegyik a szomszédja lesz; a 2-nek az 5, az 5-nek a 2 kivételével mindegyik a szomszédja lesz; a 3-nak a 4, a 4-nek a 3 kivételével mindegyik a szomszédja lesz. Pirosra tehát csak az 1-6, 2-5 vagy 3-4 oldalakat festhetjük, így a piros lapok elhelyezésére három lehetőség adódik. Bármelyik párost választjuk pirosnak, akkor a megmaradt négy négyzetet 24 különböző módon tudjuk kifesteni. Vagyis 72 különböző módon színezhető a feltételeknek megfelelő módon az ábra.

Statisztika:

133 dolgozat érkezett.
6 pontot kapott:	78 versenyző.
5 pontot kapott:	31 versenyző.
4 pontot kapott:	6 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	2 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2010. márciusi matematika feladatai