A K. 264. feladat (2010. október)

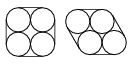
K. 264. Négy darab henger alakú konzervet rögzítenek egybe egy gyárban az ábrán látható módokon egy köréjük tekert szalagpánttal. Milyen hosszú szalagra van szükség az egyes módozatoknál, ha a hengerek alapkörének átmérője 10 cm, és a szalag záródásánál hosszában 2 cm átfedés van a szalag két végének összeragasztására?

(6 pont)

A beküldési határidő 2010. november 10-én LEJÁRT.

Megoldás. A szalagpántokat daraboljuk fel az érintési pontok mentén. Ha sem az alakjukon, sem a darabok egymással bezárt szögén nem változtatunk, csak eltoljuk őket az ábra szerint, akkor egy-egy 10cm sugarú kört, egy 20cm oldalú négyzetet, illetve rombuszt kapunk.

Mivel a négyszögek oldalai 20cm nagyságúak mindkét esetben, kerületük megegyezik: 80cm. Tehát mindkét elrendezés estén \(\displaystyle 20\pi+80+2\)cm, azaz kb. 144,832cm szalagpántra van szükség.

Statisztika:

296 dolgozat érkezett.
6 pontot kapott:	81 versenyző.
5 pontot kapott:	33 versenyző.
4 pontot kapott:	26 versenyző.
3 pontot kapott:	109 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	20 versenyző.
Nem versenyszerű:	9 dolgozat.

A KöMaL 2010. októberi matematika feladatai